题目内容
已知函数f(x)=|x-1|.
(1)解不等式f(x)+f(x+4)≤8;
(2)若|a|<1,|b|<1,且a≠0,求证:f(ab)>|a|f(
).
(1)解不等式f(x)+f(x+4)≤8;
(2)若|a|<1,|b|<1,且a≠0,求证:f(ab)>|a|f(
| b |
| a |
考点:绝对值不等式的解法
专题:不等式
分析:(1)利用函数零点将绝对值去掉,将函数转化为分段函数,分类讨论解不等式;
(2)先利用已知函数将所证结论进行转化变成|ab-1|>|a-b|,再利用作差法先证|ab-1|2-|a-b|2>0,再开方即可.
(2)先利用已知函数将所证结论进行转化变成|ab-1|>|a-b|,再利用作差法先证|ab-1|2-|a-b|2>0,再开方即可.
解答:
解:(Ⅰ)f(x)+f(x+4)=|x-1|+|x+3|=
,
当x<-3时,由-2x-2≥8,解得x≤-5;
当-3≤x≤1时,f(x)≤8不成立;
当x>1时,由2x+2≥8,解得x≥3.…(4分)
所以不等式f(x)≤4的解集为{x|x≤-5或x≥3}.…(5分)
(Ⅱ)f(ab)>|a|f(
)即|ab-1|>|a-b|.…(6分)
因为|a|<1,|b|<1,
所以|ab-1|2-|a-b|2=(a2b2-2ab+1)-(a2-2ab+b2)=(a2-1)(b2-1)>0,
所以|ab-1|>|a-b|.
故所证不等式成立.…(10分)
|
当x<-3时,由-2x-2≥8,解得x≤-5;
当-3≤x≤1时,f(x)≤8不成立;
当x>1时,由2x+2≥8,解得x≥3.…(4分)
所以不等式f(x)≤4的解集为{x|x≤-5或x≥3}.…(5分)
(Ⅱ)f(ab)>|a|f(
| b |
| a |
因为|a|<1,|b|<1,
所以|ab-1|2-|a-b|2=(a2b2-2ab+1)-(a2-2ab+b2)=(a2-1)(b2-1)>0,
所以|ab-1|>|a-b|.
故所证不等式成立.…(10分)
点评:本题考查解绝对值不等式和证明不等式,意在考查考生运用函数零点分类讨论的解题思想.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
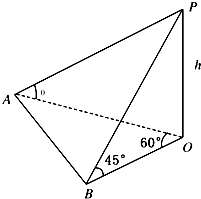 地平面上一旗杆OP,为测得它的高度h,在地平面上取一基线AB,AB=30m,在A处测得旗杆顶P点的仰角为θ且tanθ=
地平面上一旗杆OP,为测得它的高度h,在地平面上取一基线AB,AB=30m,在A处测得旗杆顶P点的仰角为θ且tanθ=| 1 |
| 2 |
设a∈R,则“a=1”是“直线l2:ax+y-1=0与直线l2:x-ay-3=0垂直”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
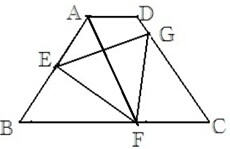 如图,梯形ABCD,AD∥BC,AB=CD=6,AD=2,BC=8,∠B=60°,点E在AB上,点F在BC上,
如图,梯形ABCD,AD∥BC,AB=CD=6,AD=2,BC=8,∠B=60°,点E在AB上,点F在BC上,