题目内容
已知双曲线与椭圆
+
=1共焦点,且以y=±
x为渐近线.
(1)求双曲线方程.
(2)求过双曲线右焦点且倾斜角为
的直线方程.
| x2 |
| 49 |
| y2 |
| 24 |
| 4 |
| 3 |
(1)求双曲线方程.
(2)求过双曲线右焦点且倾斜角为
| π |
| 3 |
考点:双曲线的简单性质,双曲线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)求出椭圆的焦点坐标,设出双曲线方程,结合以y=±
x为渐近线,求出a,b,即可得到双曲线方程.
(2)求出直线的斜率,可得过双曲线右焦点且倾斜角为
的直线方程.
| 4 |
| 3 |
(2)求出直线的斜率,可得过双曲线右焦点且倾斜角为
| π |
| 3 |
解答:
解:(1)椭圆的焦点坐标为(±5,0),设双曲线方程为
-
=1(a>0,b>0)…(1分)
则渐近线方程为y=±
x,
所以
…(4分)
解得
…(6分)
则双曲线方程为
-
=1…(7分)
(2)∵直线的倾斜角为
,
∴直线的斜率为
,…(9分)
故直线方程为y=
(x-5)…(11分)
即
x-y-5
=0…(12分)
| x2 |
| a2 |
| y2 |
| b2 |
则渐近线方程为y=±
| b |
| a |
所以
|
解得
|
则双曲线方程为
| x2 |
| 9 |
| y2 |
| 16 |
(2)∵直线的倾斜角为
| π |
| 3 |
∴直线的斜率为
| 3 |
故直线方程为y=
| 3 |
即
| 3 |
| 3 |
点评:本题考查椭圆、双曲线的性质与方程,考查学生的计算能力,属于中档题.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
“x=2”是“log2|x|=1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
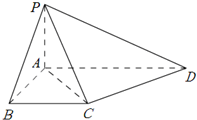 如图,在四棱锥P-ABCD,PA⊥平面ABCD,PA=AB=BC=
如图,在四棱锥P-ABCD,PA⊥平面ABCD,PA=AB=BC=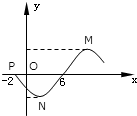 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象的一部分如图,已知函数与x轴交于点P(-2,0)和(6,0),点M,N分别是最高点和最低点,且∠MPN=
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象的一部分如图,已知函数与x轴交于点P(-2,0)和(6,0),点M,N分别是最高点和最低点,且∠MPN=