题目内容
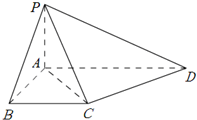 如图,在四棱锥P-ABCD,PA⊥平面ABCD,PA=AB=BC=
如图,在四棱锥P-ABCD,PA⊥平面ABCD,PA=AB=BC=| 1 |
| 2 |
(1)求证:CD⊥平面PAC;
(2)求二面角A-PD-C的余弦值.
考点:用空间向量求平面间的夹角,直线与平面垂直的判定
专题:空间角
分析:(1)过C作CE∥AB,交AD于E,由已知条件利用勾股定理求出CD⊥AC,由此能证明CD⊥平面PAC.
(2)由已知条件求出CE⊥平面PAD,过E作EF⊥PD于F,连结CF,得到∠GHC是二面角A-PD-C的平面角,同此能求出二面角A-PD-C的余弦值.
(2)由已知条件求出CE⊥平面PAD,过E作EF⊥PD于F,连结CF,得到∠GHC是二面角A-PD-C的平面角,同此能求出二面角A-PD-C的余弦值.
解答:
(1)证明:∵PA⊥平面ABCD,
∴CD⊥PA.(1分)
又∵AB=BC,∠ABC=90°,
∴AC=
AB,(2分)
过C作CE∥AB,交AD于E,
则CE=AB=BC=DE,∠CED=90°,(3分)
∴CD=
AB,(4分)
在△ACD中,AC2+CD2=4AB2=AD2,∴CD⊥AC.(5分)
又∵PA∩AC=A,∴CD⊥平面PAC.(6分)
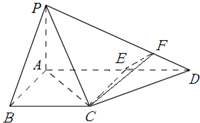 (2)解:∵CE⊥AD,CE⊥PA,
(2)解:∵CE⊥AD,CE⊥PA,
∴CE⊥平面PAD.(7分)
过E作EF⊥PD于F,连结CF,得CF⊥PD.(8分)
∴∠GHC是二面角A-PD-C的平面角.(9分)
设AD=2,则PA=AB=CE=DE=1,DP=
.
∵△PAD∽△DEF,
∴
=
,
∴EF=
.(11分)
∴CF=
=
=
,(12分)
∴cos∠CFE=
=
.
∴二面角A-PD-C的余弦值为
.(14分)
∴CD⊥PA.(1分)
又∵AB=BC,∠ABC=90°,
∴AC=
| 2 |
过C作CE∥AB,交AD于E,
则CE=AB=BC=DE,∠CED=90°,(3分)
∴CD=
| 2 |
在△ACD中,AC2+CD2=4AB2=AD2,∴CD⊥AC.(5分)
又∵PA∩AC=A,∴CD⊥平面PAC.(6分)
 (2)解:∵CE⊥AD,CE⊥PA,
(2)解:∵CE⊥AD,CE⊥PA,∴CE⊥平面PAD.(7分)
过E作EF⊥PD于F,连结CF,得CF⊥PD.(8分)
∴∠GHC是二面角A-PD-C的平面角.(9分)
设AD=2,则PA=AB=CE=DE=1,DP=
| 5 |
∵△PAD∽△DEF,
∴
| EF |
| PA |
| DE |
| DP |
∴EF=
| 1 | ||
|
∴CF=
| CE2+EF2 |
1+
|
| ||
| 6 |
∴cos∠CFE=
| EF |
| CF |
| ||
| 6 |
∴二面角A-PD-C的余弦值为
| ||
| 6 |
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
数列1,1,2,1,1,2,3,2,1,1,2,3,4,3,2,1,…,则第100项为( )
| A、1 | B、2 | C、3 | D、4 |
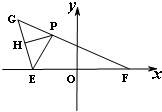 如图,在平面直角坐标系中,点E,F是x轴上的两个定点,|EO|=|OF|=
如图,在平面直角坐标系中,点E,F是x轴上的两个定点,|EO|=|OF|= 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在CE上,无论点F运动到何处时,总有BF⊥AE.
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在CE上,无论点F运动到何处时,总有BF⊥AE.