题目内容
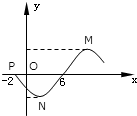函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的图象的一部分如图，已知函数与x轴交于点P（-2，0）和（6，0），点M，N分别是最高点和最低点，且∠MPN=| π |
| 2 |
（Ⅰ）求函数f（x）表达式；
（Ⅱ）若f（x0+
| 10 |
| 3 |
| 3 |
| π |
| 4 |
| π |
| 6 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：（Ⅰ）根据图象求出周期T，再由周期公式求出ω的值，再设M（10，A），N（2，-A），由题意得
•
=0，根据向量的坐标运算和数量积运算，列出方程求出A，把图象上的点坐标（2，-A）代入解析式，根据条件和特殊角的正弦值求出φ的值；
（Ⅱ）根据条件和（Ⅰ）代入后化简得：sin(
x0-
)=
，利用二倍角余弦公式求出cos(
x0-
)的值，利用诱导公式求出sin(
x0-
)的值．
| PM |
| PN |
（Ⅱ）根据条件和（Ⅰ）代入后化简得：sin(
| π |
| 8 |
| π |
| 3 |
| 1 |
| 4 |
| π |
| 4 |
| 2π |
| 3 |
| π |
| 4 |
| π |
| 6 |
解答：
解：（Ⅰ）依题意好人图象得T=16，∴T=
=16，解得ω=
，
设M（10，A），N（2，-A），
∵∠MPN=
，∴
•
=0，
∴
•
=(12，A)•(4，-A)=48-A2=0，解得A=4
，
∴f(x)=4
sin(
x+φ)
∵f（x）又过点N（2，-A），得sin(
+φ)=-1
∴φ=2kπ-
，k∈Z
∵|φ|＜π，∴φ=-
∴f(x)=4
sin(
x-
π)，
（Ⅱ）把f(x0+
)=
代入f（x）得，4
sin(
x0-
)=
，
则sin(
x0-
)=
，
∵cos(
x0-
)=cos2(
x0-
)=1-2sin2(
x0-
)=
，
∵sin(
x0-
)=cos[(
x0-
)-
]=cos(
x0-
)
∴sin(
x0-
)=
．
| 2π |
| ω |
| π |
| 8 |
设M（10，A），N（2，-A），
∵∠MPN=
| π |
| 2 |
| PM |
| PN |
∴
| PM |
| PN |
| 3 |
∴f(x)=4
| 3 |
| π |
| 8 |
∵f（x）又过点N（2，-A），得sin(
| π |
| 4 |
∴φ=2kπ-
| 3π |
| 4 |
∵|φ|＜π，∴φ=-
| 3π |
| 4 |
∴f(x)=4
| 3 |
| π |
| 8 |
| 3 |
| 4 |
（Ⅱ）把f(x0+
| 10 |
| 3 |
| 3 |
| 3 |
| π |
| 8 |
| π |
| 3 |
| 3 |
则sin(
| π |
| 8 |
| π |
| 3 |
| 1 |
| 4 |
∵cos(
| π |
| 4 |
| 2π |
| 3 |
| π |
| 8 |
| π |
| 3 |
| π |
| 8 |
| π |
| 3 |
| 7 |
| 8 |
∵sin(
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 2 |
| π |
| 4 |
| 2π |
| 3 |
∴sin(
| π |
| 4 |
| π |
| 6 |
| 7 |
| 8 |
点评：本题考查了由y=Asin（ωx+φ）的图象求解析式，向量垂直的条件，向量的坐标运算和数量积运算，以及二倍角余弦公式、诱导公式，变角是三角恒等变换的关键，考查识图能力和转化思想，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=x3-3x+a有三个零点，则a的取值范围为（ ）
| A、（-∞，-2）∪（2，+∞） |
| B、（-∞，2]∪[2，+∞） |
| C、（-2，2） |
| D、[-2，2] |
如图，四边形ABCD是边长为2的正方形，△ABE为等腰三角形，AE=BE，平面ABCD⊥平面ABE，动点F在CE上，无论点F运动到何处时，总有BF⊥AE．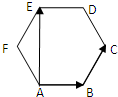
如图，在边长为1的正六边形ABCDEF中，