题目内容

已知直线l：ax-y=0在矩阵A=[
01
12
]对应的变换作用下得到直线l′，若直线l′过点（1，1），求实数a的值．
考点：旋转变换
专题：计算题,矩阵和变换
分析：直线l：ax-y=0上任意一点（x，y），（x′，y′）是所得的直线上一点，根据矩阵变换特点，写出两对坐标之间的关系，把已知的点的坐标代入得到直线的方程，得到结果．
解答： 解：设P（x，y）为直线l上任意一点，在矩阵A对应的变换下变为直线l′上点P′（x′，y′），则
x′
y′
=[
01
12
]
x
y
，
化简，得
x=-2x′+y′
y=x′
         …（4分）
代入ax-y=0，整理，得-（2a+1）x′+ay′=0．    …（8分）
将点（1，1）代入上述方程，解得a=-1．         …（10分）
点评：本题主要考查二阶矩阵的变换，考查运算求解能力，比较基础．
练习册系列答案
相关题目
过椭圆
x2
4
+
y2
3
=1的右焦点F（1，0）的直线L交椭圆于A，B两点，当△OAB面积最大时，求直线L的方程．
已知双曲线与椭圆
x2
49
+
y2
24
=1共焦点，且以y=±
4
3
x为渐近线．
（1）求双曲线方程．
（2）求过双曲线右焦点且倾斜角为
π
3
的直线方程．
如图，四边形ABCD是边长为2的正方形，△ABE为等腰三角形，AE=BE，平面ABCD⊥平面ABE，动点F在CE上，无论点F运动到何处时，总有BF⊥AE．
（Ⅰ）求证：平面ADE⊥平面BCE；
（Ⅱ）求三校锥的D-ACE体积．
已知椭圆的一个顶点为A（0，-1），焦点在x轴上，离心率e=
6
3
．
（1）求椭圆标准方程；
（2）设直线l1：y=x+m，直线l1与（1）中的椭圆有两个不同的交点M、N，求m的取值范围；
（3）直线l2：x=ty+1，t∈R与（1）中的椭圆有两个不同的交点P，Q，当△OPQ的面积S取到最大值时，求直线l2的方程．（O是坐标原点）
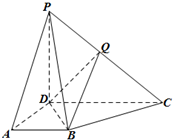在四棱锥P-ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，底面ABCD是直角梯形，AB∥CD，∠ADC=
π
2
，AB=AD=PD=1，CD=2．设Q为侧棱PC上一点，
PQ
=λ
PC
，试确定λ的值，使得二面角Q-BD-P为45°．
正三角形ABC的边长为1，且
BC
=
a
，
CA
=
b
，
AB
=
c
，求|
a
-
b
+2
c
|的值．
求函数y=log2[3-2
3
tanx-3tan2x]的定义域与值域．
已知函数f（x）对任意x∈R，都有f（x+2）•f（x）=k（k为常数），且当x∈[0，2]时，f（x）=x2+1，则f（5）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网