题目内容
已知向量
=(1,-3),
=(-1,2),
=(2,8)
(Ⅰ)若
=x
+y
,求x,y的值;
(Ⅱ)若
=3
+5
,求向量
与向量
的夹角.
| a |
| b |
| c |
(Ⅰ)若
| c |
| a |
| b |
(Ⅱ)若
| d |
| a |
| b |
| a |
| d |
考点:数量积表示两个向量的夹角,平面向量的基本定理及其意义
专题:平面向量及应用
分析:(I)利用已知向量表示出向量
,结合已知向量
的坐标及向量相等的条件可求x,y
(II)先求出向量
的坐标,然后直接代入向量的夹角余弦公式可求
| c |
| c |
(II)先求出向量
| d |
解答:
解:(Ⅰ)∵
=(1,-3),
=(-1,2),
=(2,8)且
=x
+y
∴(2,8)=x(1,-3)+y(-1,2)
∴
∴
…(6分)
(Ⅱ)∵
=3
+5
,
=(1,-3),
=(-1,2)
∴
=(-2,1)∴
•
=-5,|
|=
,|
|=
设向量
与向量
的夹角为θ
∴cosθ=
=
=-
∵θ∈[0,π],
∴θ=
…(12分)
| a |
| b |
| c |
| c |
| a |
| b |
∴(2,8)=x(1,-3)+y(-1,2)
∴
|
∴
|
(Ⅱ)∵
| d |
| a |
| b |
| a |
| b |
∴
| d |
| a |
| d |
| a |
| 10 |
| d |
| 5 |
设向量
| a |
| d |
∴cosθ=
| ||||
|
|
| -5 | ||||
|
| ||
| 2 |
∵θ∈[0,π],
∴θ=
| 3π |
| 4 |
点评:本题主要考查了向量的坐标运算及向量的夹角公式的坐标表示,属于基础试题

练习册系列答案
相关题目
已知a>0,x、y满足约束条件
,若z=2x+y的最小值为0,则a=( )
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知函数f(x)=x3-3x+a有三个零点,则a的取值范围为( )
| A、(-∞,-2)∪(2,+∞) |
| B、(-∞,2]∪[2,+∞) |
| C、(-2,2) |
| D、[-2,2] |
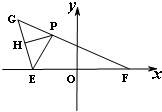 如图,在平面直角坐标系中,点E,F是x轴上的两个定点,|EO|=|OF|=
如图,在平面直角坐标系中,点E,F是x轴上的两个定点,|EO|=|OF|=