题目内容
某同学参加科普知识竞赛需回答3个问题,竞赛规则规定:答对第1、2、3个问题分别得100分、100分、200分,答错得零分.假设这名同学答对第1、2、3个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响.
(1)求这名同学得200分的概率;
(2)如果规定至少得300分则算通过,求某同学能通过竞赛的概率.
(1)求这名同学得200分的概率;
(2)如果规定至少得300分则算通过,求某同学能通过竞赛的概率.
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:应用题,概率与统计
分析:(1)由题意知各题答对与否相互之间没有影响,这名同学得200分包括两种情况,一是答对第一和第二两个题目,二是答对第三题目,这两种情况是互斥的,根据相互独立事件和互斥事件的概率公式得到结果.
(2)这名同学至少得300分包括得300分或得400分,这两种情况是互斥的,根据相互独立事件和互斥事件的概率公式得到结果.
(2)这名同学至少得300分包括得300分或得400分,这两种情况是互斥的,根据相互独立事件和互斥事件的概率公式得到结果.
解答:
解:记“这名同学答对第i个问题”为事件Ai(i=1,2,3),则P(A1)=0.8,P(A2)=0.7,P(A3)=0.6
(1)这名同学得200分的概率为:P1=P(A1A2
)+P(
A3)
0.8×0.7×0.4+0.2×0.3×0.6=0.26
(2)这名同学至少得300分的概率为:P2=P(A1
A3)+P(
A2A3)+P(A1A2A3)
=P(A1)P(
)P(A3)+P(
)P(A2)P(A3)+P(A1)P(A2)P(A3)
=0.8×0.3×0.6+0.2×0.7×0.6+0.8×0.7×0.6=0.564,
所以某同学能通过的概率为0.564
(1)这名同学得200分的概率为:P1=P(A1A2
. |
| A3 |
. |
| A1 |
. |
| A2 |
0.8×0.7×0.4+0.2×0.3×0.6=0.26
(2)这名同学至少得300分的概率为:P2=P(A1
. |
| A2 |
. |
| A1 |
=P(A1)P(
. |
| A2 |
. |
| A1 |
=0.8×0.3×0.6+0.2×0.7×0.6+0.8×0.7×0.6=0.564,
所以某同学能通过的概率为0.564
点评:本小题主要考查相互独立事件同时发生的概率,考查应用概率知识解决实际问题的能力,是一个综合题,注意对题目中出现的“至少”的理解.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
关于随机对照试验的说法,正确的是( )
| A、试验组的对象必须是随机选择出的 |
| B、对照组的对象不必随机选择出的 |
| C、不要对照组 |
| D、对照组中的对象必须使用安慰剂 |
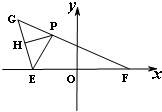 如图,在平面直角坐标系中,点E,F是x轴上的两个定点,|EO|=|OF|=
如图,在平面直角坐标系中,点E,F是x轴上的两个定点,|EO|=|OF|= 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在CE上,无论点F运动到何处时,总有BF⊥AE.
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在CE上,无论点F运动到何处时,总有BF⊥AE.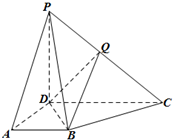 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=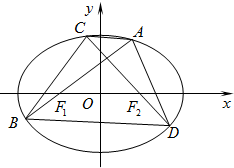 已知椭圆
已知椭圆