题目内容
已知函数f(x)=Asin2x,g(x)=
Asin(2x-
),(A>0),直线x=m与f(x),g(x)的图象分别交M、N两点,且|MN|(M、N两点间的距离)的最大值为10,则常数A的值为 .
| 3 |
| π |
| 2 |
考点:三角函数的最值
专题:三角函数的求值
分析:由已知中直线x=m分别交函数y=Asin2x、g(x)=
Asin(2x-
)的图象于M、N两点,表示M、N的距离,根据辅助角公式化为一个正弦型函数的形式,根据正弦型函数的值域,即可得到结果.
| 3 |
| π |
| 2 |
解答:
解:∵g(x)=
Asin(2x-
)=-
Acos2x,直线x=m分别交函数y=Asin2x、g(x)=
Asin(2x-
)的图象于M、N两点,
则|MN|=|Asin2x+
Acos2x|=2A|
sin2x+
cos2x|=2A|sin(2x+
)|的最大值为2A,
而已知则|MN|的最大值为10,可得2A=10,由此求得A=5,
故答案为:5.
| 3 |
| π |
| 2 |
| 3 |
| 3 |
| π |
| 2 |
则|MN|=|Asin2x+
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
而已知则|MN|的最大值为10,可得2A=10,由此求得A=5,
故答案为:5.
点评:本题考查三角函数的最值及三角函数的化简求值,本题解题的关键是构造函数表示M、N的距离,把问题转化为三角函数的最值问题,本题是一个中档题目.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
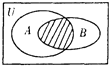
设全集U=R,A={x|x(x+2)<0,B={x|x<-1},则图中阴影部分表示的集合为( )

| A、{x|-2<x<0} |
| B、{x|-2<x<-1} |
| C、{x|x>0} |
| D、{x|x<-1} |
若sinαtanα>0,且sinαcosα<0,则α是( )
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
cos(α-35°)cos(α+25°)+sin(α-35°)sin(α+25°)等于( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知定义在[1,+∞)上的函数f(x)=
则下列结论正确的是( )
|
| A、函数f(x)的值域为[1,4] | ||
B、关于x的方程f(x)-
| ||
| C、当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的面积为3 | ||
| D、不存在实数x0,使不等式x0f(x0)>6成立 |