题目内容
已知定义在[1,+∞)上的函数f(x)=
则下列结论正确的是( )
|
| A、函数f(x)的值域为[1,4] | ||
B、关于x的方程f(x)-
| ||
| C、当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的面积为3 | ||
| D、不存在实数x0,使不等式x0f(x0)>6成立 |
考点:命题的真假判断与应用
专题:阅读型,函数的性质及应用,等差数列与等比数列
分析:由分段函数,求出1≤x≤2,2≤x≤4,4≤x≤8函数的表达式,画出草图,通过图象可知函数的值域为[0,4],
可判断A;当n=1时,f(x)-
=0有7个不相等的实根,可判断B;当x∈[2n-1,2n](n∈N*),时,函数f(x)的最高点为23-n,可求出与x轴围成的面积可判断C;函数f(x)的最高点都在曲线y=
(x>0)上,可判断D.
可判断A;当n=1时,f(x)-
| 1 |
| 2 |
| 6 |
| x |
解答:
解:当1≤x≤
时,f(x)=8x-8;
≤x≤2时,f(x)=16-8x;
设2≤x≤3,则1≤
≤
,f(x)=
f(
)=2x-4;
3≤x≤4,则
≤
≤2,f(x)=
f(
)=8-2x;
4≤x≤6,则2≤
≤3,f(x)=
f(
)=
-2;
6≤x≤8,则3≤
≤4,f(x)=
f(
)=4-
.
 画出草图,
画出草图,
知函数的值域为[0,4],
故A错;
当n=1时,f(x)-
=0在[1,8]上有6个不相等的实根,[8,16]上只有一个实根,以后再没有了,
共有7个不相等的实根,
故B错;
函数f(x)的最高点为以4为首项,公比为
的等比数列.
故当x∈[2n-1,2n](n∈N*),时,函数f(x)的最高点为23-n,与x轴围成的面积为
×23-n×2n-1=2.故C错;
函数f(x)的最高点都在曲线y=
(x>0)上,故D正确.
故选D.
| 3 |
| 2 |
| 3 |
| 2 |
设2≤x≤3,则1≤
| x |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
3≤x≤4,则
| 3 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
4≤x≤6,则2≤
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| x |
| 2 |
6≤x≤8,则3≤
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| x |
| 2 |
 画出草图,
画出草图,知函数的值域为[0,4],
故A错;
当n=1时,f(x)-
| 1 |
| 2 |
共有7个不相等的实根,
故B错;
函数f(x)的最高点为以4为首项,公比为
| 1 |
| 2 |
故当x∈[2n-1,2n](n∈N*),时,函数f(x)的最高点为23-n,与x轴围成的面积为
| 1 |
| 2 |
函数f(x)的最高点都在曲线y=
| 6 |
| x |
故选D.
点评:本题考查分段函数及运用,考查函数的表达式和值域,等比数列的通项及运用,考查数形结合的能力,判断能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=Asin2x,g(x)=
Asin(2x-
),(A>0),直线x=m与f(x),g(x)的图象分别交M、N两点,且|MN|(M、N两点间的距离)的最大值为10,则常数A的值为 .
| 3 |
| π |
| 2 |
在下列各组向量中,能作为表示它们所在平面内所有向量的基底的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等差数列{an}前n项和为Sn.又a5=6,S5=20,则数列{
}前99项的和为( )
| 2 |
| anan+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
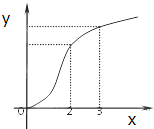

| A、0<f′(2)<f′(3)<f(3)-f(2) |
| B、0<f′(3)<f(3)-f(2)<f′(3) |
| C、0<f′(3)<f′(2)<f(3)-f(2) |
| D、0<f(3)-<f(2)<f′(2)<f′(3) |
计算cos480°=( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
已知函数f(x)=
,若方程f(x)=4有且仅有一个解,则实数a的取值范围为( )
|
| A、(0,3) |
| B、[0,3] |
| C、(1,4) |
| D、[1,4] |
在△ABC中,sinA=sinC,则△ABC是( )
| A、直角三角形 |
| B、等腰三角形 |
| C、钝角三角形 |
| D、锐角三角形 |