题目内容
| ∫ | 1 0 |
| -x2+2x |
考点：定积分
专题：导数的综合应用
分析：由差的积分等于积分的差，然后利用定积分的几何意义求得
（
）dx，则答案可求．
| ∫ | 1 0 |
| -x2+2x |
解答：
解：∵
（
-x）dx
=
（
）dx-
xdx．
由定积分的几何意义知，
（
）dx是以（1，0）为圆心，以1为半径的
圆的面积，
等于
．
而
xdx=
x2
=
．
∴
（
-x）dx=
-
．
故答案为：
-
．
| ∫ | 1 0 |
| -x2+2x |
=
| ∫ | 1 0 |
| -x2+2x |
| ∫ | 1 0 |
由定积分的几何意义知，
| ∫ | 1 0 |
| -x2+2x |
| 1 |
| 4 |
等于
| π |
| 4 |
而
| ∫ | 1 0 |
| 1 |
| 2 |
| | | 1 0 |
| 1 |
| 2 |
∴
| ∫ | 1 0 |
| -x2+2x |
| π |
| 4 |
| 1 |
| 2 |
故答案为：
| π |
| 4 |
| 1 |
| 2 |
点评：本题考查了定积分，考查了定积分的几何意义，考查了微积分基本定理，是基础题．
练习册系列答案
全能练考卷系列答案
相关题目
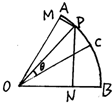如图，扇形OAB的半径为2，圆心角为