题目内容
12.用更相减损术求得81与135的最大公约数是( )| A. | 54 | B. | 27 | C. | 9 | D. | 81 |
分析 利用更相减损术即可得出.
解答 解:135-81=54,81-54=27,54-27=27,.
∴81与135的最大公约数是27.
故选:B.
点评 本题考查了更相减损术的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知双曲线的一条渐近线方程为y=4x,且双曲线的焦点与抛物线y2=8x的焦点是重合的,则双曲线的标准方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{{17{x^2}}}{4}-\frac{{17{y^2}}}{64}=1$ | ||
| C. | $\frac{x^2}{4}-\frac{{4{y^2}}}{5}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{2}=1$ |
3.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线方程$y=\sqrt{3}x$,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
17.双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点为F(c,0),若圆C:(x-c)2+y2=4a2与双曲线E的渐近线相切,则E的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
4.双曲线$\frac{x^2}{4}-\frac{y^2}{5}=1$的焦距等于( )
| A. | 2 | B. | 4 | C. | 3 | D. | 6 |
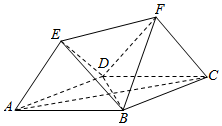 如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.
如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.