题目内容
下列命题中的真命题是( )
①若命题p:?x<0,x≥sinx,命题q:函数f(x)=x2-2x仅有两个零点,则命题¬p∨q为真命题;
②若变量x,y的一组观测数据(x1,y1),(x2,y2),…,(xn,yn)均在直线y=2x+1上,则y与x的线性相关系数r=1;
③若a,b∈[0,1],则使不等式a+b<
成立的概率是
.
①若命题p:?x<0,x≥sinx,命题q:函数f(x)=x2-2x仅有两个零点,则命题¬p∨q为真命题;
②若变量x,y的一组观测数据(x1,y1),(x2,y2),…,(xn,yn)均在直线y=2x+1上,则y与x的线性相关系数r=1;
③若a,b∈[0,1],则使不等式a+b<
| 1 |
| 2 |
| 1 |
| 4 |
| A、①② | B、??①③ |
| C、?② | D、??②③ |
考点:命题的真假判断与应用
专题:简易逻辑
分析:对于①,判断命题p为假命题,则¬p为真命题,命题q为假命题,由复合命题的真假得到命题¬p∨q为真命题;
对于②,由完全相关的相关系数等于1得到命题正确;
等于③,由几何概型求出概率,判断命题错误.
对于②,由完全相关的相关系数等于1得到命题正确;
等于③,由几何概型求出概率,判断命题错误.
解答:
解:对于①,
∵x∈(0,
)时,恒有x>sinx,
∴x<0时,x<sinx,命题p为假命题,则命题¬p为真命题.
函数f(x)=x2-2x一定有一个小于0的零点,有两个大于0的零点2,4,
∴命题q为假命题.
则命题¬p∨q为真命题正确;
对于②,若变量x,y的一组观测数据(x1,y1),(x2,y2),…,(xn,yn)均在直线y=2x+1上,
则变量x,y具有完全相关关系,y与x的线性相关系数r=1,命题②正确;
对于③,∵a,b∈[0,1],如图,
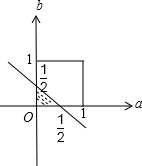
则使不等式a+b<
成立的概率是
=
.
命题③错误.
∴正确的命题是①②.
故选:A.
∵x∈(0,
| π |
| 2 |
∴x<0时,x<sinx,命题p为假命题,则命题¬p为真命题.
函数f(x)=x2-2x一定有一个小于0的零点,有两个大于0的零点2,4,
∴命题q为假命题.
则命题¬p∨q为真命题正确;
对于②,若变量x,y的一组观测数据(x1,y1),(x2,y2),…,(xn,yn)均在直线y=2x+1上,
则变量x,y具有完全相关关系,y与x的线性相关系数r=1,命题②正确;
对于③,∵a,b∈[0,1],如图,

则使不等式a+b<
| 1 |
| 2 |
| ||||||
| 1 |
| 1 |
| 8 |
命题③错误.
∴正确的命题是①②.
故选:A.
点评:本题考查命题的真假判断与应用,考查了复合命题的真假判断,考查了两个变量的完全相关性,训练了几何概型概率的求法,是中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
等比数列{an]中,“a1<a3”是“a4<a6”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
若直线y=2x+b被圆(x+1)2+y2=4所截得的弦最长,则b等于( )
| A、-1 | B、0 | C、1 | D、2 |
一个几何体三视图如图所示,则这个几何体体积等于( )


A、
| ||
| B、2 | ||
| C、1 | ||
| D、4 |
如图是一个组合几何体的三视图,则该几何体的体积是( )


A、
| ||||
B、
| ||||
| C、12+64π | ||||
| D、36+128π |
 如图,两圆相交于点B、B1,直线PB与PB1分别于两圆交于点A,C和A1,C1,PA=AB=BC=
如图,两圆相交于点B、B1,直线PB与PB1分别于两圆交于点A,C和A1,C1,PA=AB=BC=