题目内容
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=4,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=4,AD=2,PA=2,PD=2| 2 |
(Ⅰ)证明AD⊥PB;
(Ⅱ)求二面角P-BD-A的余弦值.
考点:二面角的平面角及求法
专题:空间角
分析:(Ⅰ)由已知条件利用勾股定理推导出AD⊥PA,利用矩形性质得到AD⊥AB,由此证明AD⊥平面PAB,从而得到AD⊥PB.
(Ⅱ)过点P伯PH⊥AB于H,过点H作HE⊥BD于E,连结PE,由题设条件推导出∠PEH是二面角P-BD-A的平面角,由此能求出二面角P-BD-A的余弦值.
(Ⅱ)过点P伯PH⊥AB于H,过点H作HE⊥BD于E,连结PE,由题设条件推导出∠PEH是二面角P-BD-A的平面角,由此能求出二面角P-BD-A的余弦值.
解答:
(Ⅰ)证明:∵在△PAD中,由题设PA=AD=2,PD=
,
∴PA2+AD2=PD2,
∴AD⊥PA,
∵在矩形ABCD中,AD⊥AB,又PA∩AB=A,
∴AD⊥平面PAB,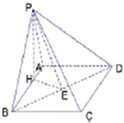
∵PB?平面PAB,∴AD⊥PB.
(Ⅱ)过点P伯PH⊥AB于H,过点H作HE⊥BD于E,连结PE,
∵AD⊥平面PAB,PH?平面PAB,∴AD⊥PH,
又∵AD∩AB=A,
∴PH⊥平面ABCD,BD?平面ABCD,
∴PH⊥BD,HE⊥BD,PH∩HE=H,
∴BD⊥平面PHE,BD⊥PE,
从而∠PEH是二面角P-BD-A的平面角,
PH=PA•sin60°=
,AH=PAcos60°=1,
BH=AB-AH=3,BD=
=2
,
HE=
•BH=
,PE=
=
,
∴在Rt△PHE中,cos∠PEH=
=
,
∴二面角P-BD-A的余弦值为
.
| 2 |
∴PA2+AD2=PD2,
∴AD⊥PA,
∵在矩形ABCD中,AD⊥AB,又PA∩AB=A,
∴AD⊥平面PAB,

∵PB?平面PAB,∴AD⊥PB.
(Ⅱ)过点P伯PH⊥AB于H,过点H作HE⊥BD于E,连结PE,
∵AD⊥平面PAB,PH?平面PAB,∴AD⊥PH,
又∵AD∩AB=A,
∴PH⊥平面ABCD,BD?平面ABCD,
∴PH⊥BD,HE⊥BD,PH∩HE=H,
∴BD⊥平面PHE,BD⊥PE,
从而∠PEH是二面角P-BD-A的平面角,
PH=PA•sin60°=
| 3 |
BH=AB-AH=3,BD=
| AB2+AD2 |
| 5 |
HE=
| AD |
| BD |
| 3 | ||
|
| PH2+HE2 |
2
| ||
| 5 |
∴在Rt△PHE中,cos∠PEH=
| HE |
| PE |
| ||
| 4 |
∴二面角P-BD-A的余弦值为
| ||
| 4 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知函数y=f(x),数列{an}的通项公式是an=f(n),n∈N*,那么“函数y=f(x)在[1,+∞﹚上单调递增”是“数列{an}是递增数列”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下列函数是奇函数的是( )
| A、f(x)=-|x| |
| B、f(x)=lg(1+x)-lg(1-x) |
| C、f(x)=2x+2-x |
| D、f(x)=x3-1 |
 如图,有一条光线沿直线y=4射到抛物线y2=4x上的一点P,经抛物线反射后,反射光线与抛物线的交于另一点Q,O是抛物线的顶点,F是抛物线的焦点,求弦PQ的斜率和△OPQ的面积.
如图,有一条光线沿直线y=4射到抛物线y2=4x上的一点P,经抛物线反射后,反射光线与抛物线的交于另一点Q,O是抛物线的顶点,F是抛物线的焦点,求弦PQ的斜率和△OPQ的面积.