题目内容
给出如下四个命题:
①若“p且q”为假命题,则p,q均为假命题;
②命题“若a>b,则a3>b3”的否命题为“若a≤b,则a3≤b3”;
③“?x∈R,x2+1≥1”的否定是“?x∈R,x2+1≤1”;
④在△ABC中,“A>B”是“sinA>sinB”的充要条件.
其中正确的命题序号是( )
①若“p且q”为假命题,则p,q均为假命题;
②命题“若a>b,则a3>b3”的否命题为“若a≤b,则a3≤b3”;
③“?x∈R,x2+1≥1”的否定是“?x∈R,x2+1≤1”;
④在△ABC中,“A>B”是“sinA>sinB”的充要条件.
其中正确的命题序号是( )
| A、①② | B、②④ | C、②③ | D、①④ |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①根据复合命题与简单命题之间的关系进行判断.②根据否命题的定义进行判断.③根据含有量词的命题的否定进行判断.④根据正弦定理及充要条件的定义进行判断.
解答:
解:①若“p且q”为假命题,则p、q至少有一个为假命题,∴①错误.
②根据命题的否命题可知,命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”,∴②正确.
③全称命题的否定是特称命题,得③“?x∈R,x2+1≥1”的否定是“?x∈R,x2+1<1”.∴③错误.
④在△ABC中,sinA>sinB?sinA•2R>sinB•2R?a>b?A>B,∴④正确;
故②④正确;
故选:B.
②根据命题的否命题可知,命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”,∴②正确.
③全称命题的否定是特称命题,得③“?x∈R,x2+1≥1”的否定是“?x∈R,x2+1<1”.∴③错误.
④在△ABC中,sinA>sinB?sinA•2R>sinB•2R?a>b?A>B,∴④正确;
故②④正确;
故选:B.
点评:本题主要考查四种命题之间的关系,复合命题与简单命题之间的关系以及含有量词的命题的否定,充要条件的定义,比较基础.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
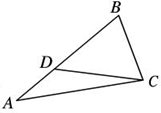 如图,D是△ABC的边AB的三等分点,则向量
如图,D是△ABC的边AB的三等分点,则向量| CD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知f(x)=sin(x+
),g(x)=cos(x-
),则下列结论正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、函数y=f(x)•g(x)的最大值为1 | ||||
B、函数y=f(x)•g(x)的对称中心是(
| ||||
C、将f(x)的图象向右平移
| ||||
D、当x∈[-
|
已知直线AB外的任一点O,下列条件中能确定点C与点A、B一定共线的是( )
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
已知在xoy平面内有一区域M,命题甲:点(a,b)∈{(x,y||x-1|+|y-2|<2)};命题乙:点(a,b)∈M,如果甲是乙的必要条件,那么区域M的面积有( )
| A、最小值8 | B、最大值8 |
| C、最小值4 | D、最大值4 |
复数
(-2-i)+
的虚部是( )
| 1 |
| 5 |
| 1 |
| 1-2i |
A、
| ||
B、
| ||
C、-
| ||
D、-
|