题目内容
过已知圆x2+y2-x+2y+
=0的圆心,且与直线x+y+1=0垂直的直线的一般方程为 .
| 1 |
| 4 |
考点:圆的一般方程
专题:直线与圆
分析:首先把圆的一般式转化成标准式,进一步求出圆心坐标,利用点斜式求出直线方程.
解答:
解:已知已知圆x2+y2-x+2y+
=0的方程转化为:(x-
)2+(y+1)2=1,
所以:圆心坐标为(
,-1),
所以经过圆心,斜率为1的直线方程为:y+1=x-
,
即x-y-
=0.
故答案为:x-y-
=0
| 1 |
| 4 |
| 1 |
| 2 |
所以:圆心坐标为(
| 1 |
| 2 |
所以经过圆心,斜率为1的直线方程为:y+1=x-
| 1 |
| 2 |
即x-y-
| 3 |
| 2 |
故答案为:x-y-
| 3 |
| 2 |
点评:本题考查的知识要点:圆的一般方程与标准方程的转化,点斜式直线方程的应用.属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
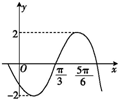 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图,则f(x)的表达式为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图,则f(x)的表达式为( )A、f(x)=2sin(
| ||||
B、f(x)=2sin(x-
| ||||
C、f(x)=2sin(
| ||||
D、f(x)=2sin(2x-
|
对任意的x∈[-2,1]时,不等式x2+2x-a≤0恒成立,则实数a的取值范围是( )
| A、(-∞,0] |
| B、(-∞,3] |
| C、[0,+∞) |
| D、[3,+∞) |
若函数f(x)=
是R上的增函数,则实数a的取值范围为( )
|
| A、(1,+∞) |
| B、(1,8) |
| C、[4,8) |
| D、(4,8) |