题目内容
8.△ABC的内角A,B,C的对边分别为a,b,c,且cosA•cosC-cos(A+C)=sin2B.(Ⅰ)证明:a,b,c成等比数列;
(Ⅱ)若角B的平分线BD交AC于点D,且b=6,S△BAD=2S△BCD,求BD.
分析 (Ⅰ)利用两角和的余弦函数公式化简已知等式可得sinAsinC=sin2B,由正弦定理可得:b2=ac,即可得证.
(Ⅱ)由已知可得:AD+CD=6,由三角形面积公式可得AD=2CD,从而可求AD=4,CD=2,由(Ⅰ)可得:b2=36,利用角平分线的性质可得AB=2BC,即c=2a,从而可求a,c的值,进而利用余弦定理可求cosA,即可由余弦定理求得BD的值.
解答 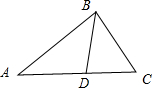 (本题满分为12分)
(本题满分为12分)
解:(Ⅰ)证明:∵cosA•cosC-cos(A+C)=sin2B.
∴cosA•cosC-(cosAcosC-sinAsinC)=sin2B,可得:sinAsinC=sin2B,
∴由正弦定理可得:b2=ac,
∴a,b,c成等比数列;
(Ⅱ)如图,∵角B的平分线BD交AC于点D,且b=6,可得:AD+CD=6,
∵S△BAD=2S△BCD,可得:AD=2CD,
∴解得:AD=4,CD=2,
∵由(Ⅰ)可得:b2=ac=36,
∵$\frac{AB}{BC}$=$\frac{AD}{DC}=\frac{4}{2}$,可得:AB=2BC,即c=2a,
∴解得:a=3$\sqrt{2}$,c=6$\sqrt{2}$,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{5\sqrt{2}}{8}$,
∴BD=$\sqrt{{c}^{2}+A{D}^{2}-2c•AD•cosA}$=2$\sqrt{7}$.
点评 本题主要考查了两角和的余弦函数公式,正弦定理,三角形面积公式,角平分线的性质,余弦定理在解三角形中的应用,考查了转化思想和数形结合思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )
某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )
 某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )
某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )| A. | n<2017 | B. | n≤2017 | C. | n>2017 | D. | n≥2017 |
19.已知实数a,b,c满足 ${(\frac{1}{3})^x}=2,{log_3}b=\frac{1}{2},{c^{-3}}=2$,则实数a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
16.已知命题p:|x-a|<4,命题q:(x-2)(3-x)>0.若¬p是¬q的充分不必要条件,则实数a的取值范围是( )
| A. | [-1,6] | B. | (-∞,-1) | C. | (6,+∞) | D. | (-∞,-1)∪(6,+∞) |
3.已知Sn为数列{an}的前n项和且Sn=2an-2,则S5-S4的值为( )
| A. | 8 | B. | 10 | C. | 16 | D. | 32 |
13.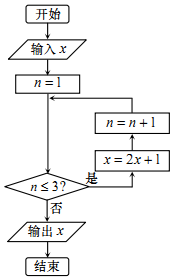 已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )
已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )
 已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )
已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
17.已知集合M={x|x2-x≤0,x∈Z},N={x|x=2n,n∈N},则M∩N为( )
| A. | {0} | B. | {1} | C. | {0,1} | D. | {0,1,2} |
16.已知函数f(x)=2sin(ωx+$\frac{π}{6}$)(ω>0)的周期为π,则下列选项正确的是( )
| A. | 函数f(x)的图象关于点($\frac{π}{6}$,0)对称 | B. | 函数f(x)的图象关于点(-$\frac{π}{12}$,0)对称 | ||
| C. | 函数f(x)的图象关于直线x=$\frac{π}{3}$对称 | D. | 函数f(x)的图象关于直线x=-$\frac{π}{12}$对称 |