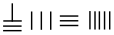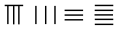题目内容
13.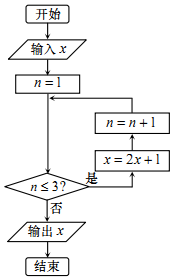 已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )
已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
分析 由框图的流程依次计算程序运行的结果,直到不满足条件,计算输出x的值,根据框图的运算结果求出当输入x∈[1,10]时,输出x的集合,并确定数集的长度,再求出输出x不大于63的数集的长度,利用长度之比求概率.
解答 解:设实数x∈[1,10],
经过第一次循环得到x=2x+1,n=2
经过第二循环得到x=2(2x+1)+1,n=3
经过第三次循环得到x=2[2(2x+1)+1]+1,n=4此时输出x
输出的值为8x+7,
∴当输入x∈[1,10]时,输出x∈[15,87],数集的长度为72;
输出x不大于63,则x∈[15,63],数集的长度为48.
∴输出的x不大于63的概率为$\frac{48}{72}$=$\frac{2}{3}$.
故选:D.
点评 本题考查了循环结构的程序框图,考查了几何概型的概率计算,根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法,求得输出x所在数集的长度是关键,属于基础题.

练习册系列答案
相关题目
3.已知集合$M=\{x|y=\sqrt{-{x^2}+2x+8}\}$,集合N={y|y=|x|+1},则M∩N=( )
| A. | {x|-2≤x≤4} | B. | {x|x≥1} | C. | {x|1≤x≤4} | D. | {x|x≥-2} |
1.已知集合A={x|$\frac{1}{2}$<2x≤2},B={x|ln(x-$\frac{1}{2}$)≤0},则A∩(∁RB)=( )
| A. | ∅ | B. | (-1,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,1) | D. | (-1,1] |
18.已知双曲线 C1:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1( a>0,b>0),圆 C2:x2+y2-2ax+$\frac{3}{4}$a2=0,若双曲线C1 的一条渐近线与圆 C2 有两个不同的交点,则双曲线 C1 的离心率的范围是( )
| A. | (1,$\frac{{2\sqrt{3}}}{3}$) | B. | ($\frac{{2\sqrt{3}}}{3}$,+∞) | C. | (1,2) | D. | (2,+∞) |
2.某位股民购进某只股票,在接下来的交易时间内,他的这只股票先经历了5次涨停(每次上涨10%),又经历了5次跌停(每次下跌10%),则该股民这只股票的盈亏情况(不考虑其他费用)为( )
| A. | 略有盈利 | B. | 略有亏损 | ||
| C. | 没有盈利也没有亏损 | D. | 无法判断盈亏情况 |
 中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如图,当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推.例如 6613 用算筹表示就是
中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如图,当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推.例如 6613 用算筹表示就是 ,则 8335 用算筹可表示为( )
,则 8335 用算筹可表示为( )