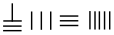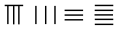题目内容
20.设随机变量ξ~N(μ,σ2),且 P (ξ<-3)=P(ξ>1)=0.2,则 P(-1<ξ<1)=0.3.分析 ξ~N(μ,σ2),且 P (ξ<-3)=P(ξ>1)=0.2,可得μ=-1,P(-1<ξ<1)=0.5-0.2=0.3.
解答 解:∵ξ~N(μ,σ2),且 P (ξ<-3)=P(ξ>1)=0.2,
∴μ=-1,P(-1<ξ<1)=0.5-0.2=0.3,
故答案为:0.3.
点评 本题考查正态分布,正态曲线有两个特点:(1)正态曲线关于直线x=μ对称;(2)在正态曲线下方和x轴上方范围内的区域面积为1.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
11.命题“?x∈R,都有x2≥0”的否定为( )
| A. | 不存在x0∈R,使得$x_0^2<0$ | B. | ?x∈R,都有x2<0 | ||
| C. | ?x0∈R,使得$x_0^2≥0$ | D. | ?x0∈R,使得$x_0^2<0$ |
15.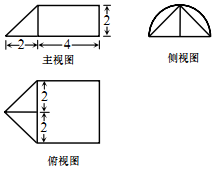 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{8}{3}$+8π | B. | $\frac{16}{3}$+8π | C. | $\frac{8}{3}$+16π | D. | $\frac{16}{3}$+16π |
8.记复数z的共轭复数为$\overline{z}$,若$\overline{z}$(1-i)=2i(i为虚数单位),则复数z的模|z|=( )
| A. | $\sqrt{2}$ | B. | 1 | C. | 2$\sqrt{2}$ | D. | 2 |
 中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如图,当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推.例如 6613 用算筹表示就是
中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如图,当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推.例如 6613 用算筹表示就是 ,则 8335 用算筹可表示为( )
,则 8335 用算筹可表示为( )