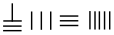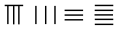题目内容
16．已知命题p：|x-a|＜4，命题q：（x-2）（3-x）＞0．若￢p是￢q的充分不必要条件，则实数a的取值范围是（ ）| A． | [-1，6] | B． | （-∞，-1） | C． | （6，+∞） | D． | （-∞，-1）∪（6，+∞） |
分析 求出命题p，q的等价条件，利用￢p是￢q的充分不必要条件，转化为q是p的充分不必要条件，即可求出a的取值范围．
解答 解：∵|x-a|＜4，
∴a-4＜x＜a+4，
即p：a-4＜x＜a+4，
∵（x-2）（x3-x）＞0，
∴2＜x＜3，
即q：2＜x＜3．
∵￢p是￢q的充分不必要条件，
∴q是p的充分不必要条件，
即 $\left\{\begin{array}{l}{a+4≥3}\\{a-4≤2}\end{array}\right.$，（等号不能同时取得），
即 $\left\{\begin{array}{l}{a≥-1}\\{a≤6}\end{array}\right.$，
∴-1≤a≤6，故选：A．
点评 本题主要考查充分条件和必要条件的应用，利用不等式的解法求出等价条件是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．命题“?x∈R，都有x2≥0”的否定为（ ）
| A． | 不存在x0∈R，使得$x_0^2＜0$ | B． | ?x∈R，都有x2＜0 | ||
| C． | ?x0∈R，使得$x_0^2≥0$ | D． | ?x0∈R，使得$x_0^2＜0$ |
1．已知集合A={x|$\frac{1}{2}$＜2x≤2}，B={x|ln（x-$\frac{1}{2}$）≤0}，则A∩（∁RB）=（ ）
| A． | ∅ | B． | （-1，$\frac{1}{2}$] | C． | [$\frac{1}{2}$，1） | D． | （-1，1] |
中国有个名句“运筹帷幄之中，决胜千里之外”，其中的“筹”原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式，如图，当表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，以此类推．例如 6613 用算筹表示就是
，则 8335 用算筹可表示为（ ）
4．下列函数在定义域中既是奇函数又是增函数的是（ ）
| A． | y=2x | B． | y=-x3 | C． | $y=3{x^{\frac{1}{3}}}$ | D． | $y=x+\frac{1}{x}$ |