题目内容
已知圆的极坐标方程为ρ=2cosθ,则它所对应的参数方程为( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:计算题,坐标系和参数方程
分析:将极坐标方程为ρ=2cosθ,化为直角坐标方程,再求出对应的参数方程.
解答:
解:∵圆的极坐标方程为ρ=2cosθ,
∴ρ2=2ρcosθ
∵x=ρcosθ,y=ρsinθ,ρ2=x2+y2,
∴消去ρ和θ得,(x-1)2+y2=1,
∴对应的参数方程为
(θ为参数),
故选:C.
∴ρ2=2ρcosθ
∵x=ρcosθ,y=ρsinθ,ρ2=x2+y2,
∴消去ρ和θ得,(x-1)2+y2=1,
∴对应的参数方程为
|
故选:C.
点评:此题考查参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,这也是每年高考必考的热点问题.

练习册系列答案
相关题目
已知关于x的方程x2-2(k-1)x+k2=0有两个实数根x1,x2,若|x1+x2|=x1x2-1,则k的值是( )
| A、-3 | B、1 | C、-3或1 | D、-1 |
下列函数是偶函数且在区间(-∞,0)上为增函数的是( )
| A、y=2x | ||
B、y=
| ||
| C、y=|x| | ||
| D、y=-x2 |
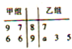 如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩,乙组记录中有一个数据模糊,无法确认,在图中以a表示,已知甲、乙两小组的数学成绩的平均分相同,则a=
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩,乙组记录中有一个数据模糊,无法确认,在图中以a表示,已知甲、乙两小组的数学成绩的平均分相同,则a=