题目内容
已知a>0,且a≠1,设p:函数y=aX在R上单调递减,Q:函数f(x)=x2-2ax+1在(
,+∞)上为增函数,“P∧Q”为假,“P∨Q”为真,求实数a的取值范围.
| 1 |
| 2 |
考点:复合命题的真假
专题:简易逻辑
分析:首先根据两个命题都真命题时,求出a的取值范围,然后,根据由“P∧Q”为假,P∨Q为真知P和Q有且只有一个为真.进行讨论,完成求解过程.
解答:
解:根据题意,
p真:0<a<1,
Q真:0<a≤
,
由“P∧Q”为假,P∨Q为真知P和Q有且只有一个为真.
(1)当P真Q假时,{a|0<a<1}∩{a?a>
且a≠1}={a?
<a<1}
(2)当P假Q真时{a?a>1}∩{a|0<a≤
}=?
综上可知:
<a<1.
∴实数a的取值范围(
,1).
p真:0<a<1,
Q真:0<a≤
| 1 |
| 2 |
由“P∧Q”为假,P∨Q为真知P和Q有且只有一个为真.
(1)当P真Q假时,{a|0<a<1}∩{a?a>
| 1 |
| 2 |
| 1 |
| 2 |
(2)当P假Q真时{a?a>1}∩{a|0<a≤
| 1 |
| 2 |
综上可知:
| 1 |
| 2 |
∴实数a的取值范围(
| 1 |
| 2 |
点评:本题重点考查了复合命题的真值表和判断、命题的真假判断等知识,属于中档题.

练习册系列答案
相关题目
若y=f(2x)的图象关于直线x=
和x=
(b>a)对称,则f(x)的一个周期为( )
| a |
| 2 |
| b |
| 2 |
A、
| ||
| B、2(b-a) | ||
C、
| ||
| D、4(b-a) |
已知数列{an}是等比数列,Sn是其前n项和,且a3=2,S3=6,则a5=( )
A、2或-
| ||
B、
| ||
| C、±2 | ||
D、2或
|
已知i是虚数单位,若复数Z=a+bi(a,b∈R)在复平面内对应的点位于第四象限,则复数Z•i在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
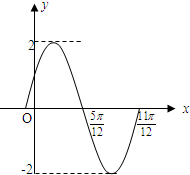 已知函数f(x)=A(sinωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.
已知函数f(x)=A(sinωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.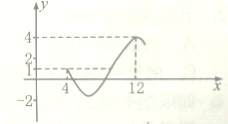 如图为函数f(x)=Asin(ωx+φ)+C(A>0,ω>0,0<φ<π)图象的一部分.
如图为函数f(x)=Asin(ωx+φ)+C(A>0,ω>0,0<φ<π)图象的一部分.