题目内容
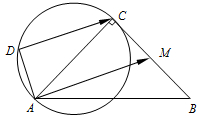 如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则
如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则| AM |
| DC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:建立适当的直角坐标系,求出相关点的坐标,求出
与
,然后求解
•
的表达式,求出最大值即可.
| AM |
| DC |
| AM |
| DC |
解答:
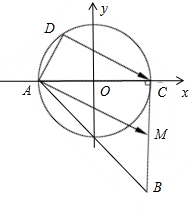 解:建立如图所示的直角坐标系,则A(-2,0),C
解:建立如图所示的直角坐标系,则A(-2,0),C
(2,0),O(0,0),M(2,-2),设D(2cosα,2sinα).
∴
=(4,-2),
=(2-2cosα,-2sinα).
•
=4×(2-2cosα)+4sinα
=8-8cosα+4sinα
=8+4
sin(α-θ),其中tanθ=2.
sin(α-θ)∈[-1,1],
∴
•
的最大值是8+4
.
故答案为:8+4
.
 解:建立如图所示的直角坐标系,则A(-2,0),C
解:建立如图所示的直角坐标系,则A(-2,0),C(2,0),O(0,0),M(2,-2),设D(2cosα,2sinα).
∴
| AM |
| DC |
| AM |
| DC |
=8-8cosα+4sinα
=8+4
| 5 |
sin(α-θ)∈[-1,1],
∴
| AM |
| DC |
| 5 |
故答案为:8+4
| 5 |
点评:本题给出直角三角形内的动点,求向量数量的最大值,着重考查了解三角形和平面向量的数量积公式等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
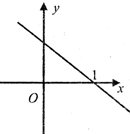 函数f(x)的导函数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),若|a-1|<|b-1|,则f(a)与f(b)的大小关系为( )
函数f(x)的导函数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),若|a-1|<|b-1|,则f(a)与f(b)的大小关系为( )| A、f(a)>f(b) |
| B、f(a)<f(b) |
| C、f(a)=f(b) |
| D、无法确定 |
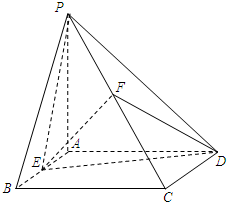 如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD.△PAD为等腰直角三角形,且PA⊥AD. E,F分别为底边AB和侧棱PC的中点.
如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD.△PAD为等腰直角三角形,且PA⊥AD. E,F分别为底边AB和侧棱PC的中点.