题目内容
在△ABC中,D是BC的中点,AD=8,BC=20,则
•
的值为 .
| AB |
| AC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据两个向量的加减法的法则,以及其几何意义,把要求的式子化为
2+
•
+
•
+
•
,再利用两个向量的数量积的定义,计算求得结果.
| AD |
| AD |
| DC |
| DB |
| AD |
| DB |
| DC |
解答:
解:由题意可得
•
=(
+
)•(
+
)
=
2+
•
+
•
+
•
=82+(8×10×cos∠ADC+8×10×cos∠ADB)+10×10×cos0
=64+0-100
=-36,
故答案为:-36.
| AB |
| AC |
| AD |
| DB |
| AD |
| DC |
=
| AD |
| AD |
| DC |
| DB |
| AD |
| DB |
| DC |
=82+(8×10×cos∠ADC+8×10×cos∠ADB)+10×10×cos0
=64+0-100
=-36,
故答案为:-36.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于中档题.

练习册系列答案
相关题目
若实数x,y满足不等式组
,则|x+y|的最小值为( )
|
| A、3 | B、-1 | C、1 | D、2 |
执行如图所示的程序框图,则输出的结果是( )


| A、5 | B、7 | C、9 | D、11 |
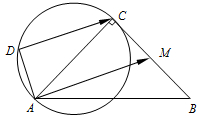 如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则
如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则