题目内容

已知P是直线3x+4y+8=0上的动点，C是圆x2+y2-2x-2y+1=0的圆心，那么|PC|的最小值是
 
．
考点：直线与圆的位置关系
专题：直线与圆
分析：将圆方程化为标准方程，得出圆心C坐标，利用点到直线的距离公式求出圆心C到直线的距离，根据垂线段最短即可得到|PC|的最小值．
解答： 解：由圆方程化为变形方程得：（x-1）2+（y-1）2=1，
∴圆心C（1，1），
∵圆心C到直线3x+4y+8=0的距离d=
|3+4+8|
32+42
=3，
∴|PC|的最小值为3．
故答案为：3
点评：此题考查了直线与圆的位置关系，解题的关键是：根据题意得出|PC|的最小值即为圆心C到已知直线的距离．
练习册系列答案
相关题目
某园艺师培育了两种珍稀树苗A与B，株数分别为12与18，现将这30株树苗的高度编写成如茎叶图（单位：cm）：

在这30株树苗中，树高在175cm以上（包括175cm）定义为“生长良好”，树高在175cm以下（不包括175cm）定义为“非生长良好”，且只有“B生长良好”的才可以出售．
（1）对于这30株树苗，如果用分层抽样的方法从“生长良好”和“非生长良好”中共抽取5株，再从这5株中任选2株，那么至少有一株“生长良好”的概率是多少？
（2）若从所有“生长良好”中选3株，用X表示所选中的树苗中能出售的株树，试写出X的分布列，并求X的数学期望．
设u=（x，y）=|ex-y|-y|x-lny|，x，y∈R．
（1）若a＞0，令f（x）=（x，a），判断f（x）的单调性；
（2）若0＜a＜b，令F（x）=u（x，a）-u（x，b），试求函数F（x）的最小值；
（3）记（2）中的最小值为T（a，b），证明：T（a，b）＞0．
已知f（x）是定义在R上的奇函数，当0≤x≤1时，f（x）=x2，当x＞1时，f（x+1）=f（x）+f（1），且若直线y=kx与函数y=f（x）的图象恰有5个不同的公共点，则实数k的值为
 
．
设圆C：x2+y2=1，直线l：x+y=2，则圆心C到直线l的距离等于
 
．
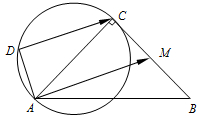如图，已知：|AC|=|BC|=4，∠ACB=90°，M为BC的中点，D为以AC为直径的圆上一动点，则
AM
•
DC
的最大值是
 
．
在数列{an}中，已知a1=1，an+1=-
1
an+1
，记Sn为数列{an}的前n项和，则S2014=
 
．
执行如图所示的程序框图，则输出的结果是（　　）
A、5B、7C、9D、11
已知：a≥2，x∈R．求证：|x-1+a|+|x-a|≥3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网