题目内容
已知数列{an}的前n项和为Sn,a1=2,nan+1=Sn+n(n+1) (n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=
,求数列{bn}的前n项和为Tn.
(1)求数列{an}的通项公式;
(2)设bn=
| 1 |
| anan+1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)nan+1=Sn+n(n+1)①⇒n≥2时,(n-1)an=Sn-1+n(n-1)②,两式相减可得an+1-an=2(n≥2),再计算a2-a1=2,从而知数列{an}是以2为首项,以2为公差的等差数列,从而可得其通项公式;
(2)利用裂项法知bn=
=
(
-
),从而可求数列{bn}的前n项和为Tn.
(2)利用裂项法知bn=
| 1 |
| anan+1 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(1)∵nan+1=Sn+n(n+1),①
∴n≥2时,(n-1)an=Sn-1+n(n-1),②
①-②得:nan+1-(n-1)an=an+2n(n≥2),
即an+1-an=2(n≥2).
在①中令n=1,有a2=a1+2,即a2-a1=2,
故对?n∈N*,an+1-an=2.
∴数列{an}是以2为首项,以2为公差的等差数列,an=2n,n∈N*.
(2)∵bn=
=
=
(
-
),
∴Tn=b1+b2+…+bn
=
[(1-
)+(
-
)+…+(
-
)]
=
.
∴n≥2时,(n-1)an=Sn-1+n(n-1),②
①-②得:nan+1-(n-1)an=an+2n(n≥2),
即an+1-an=2(n≥2).
在①中令n=1,有a2=a1+2,即a2-a1=2,
故对?n∈N*,an+1-an=2.
∴数列{an}是以2为首项,以2为公差的等差数列,an=2n,n∈N*.
(2)∵bn=
| 1 |
| anan+1 |
| 1 |
| 4n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=b1+b2+…+bn
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=
| n |
| 4n+4 |
点评:本题考查数列的求和,着重考查等差关系的确定及其通项公式的应用,突出裂项法求和的考查,属于中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
执行如图的程序框图输出的T的值为( )


| A、4 | B、6 | C、8 | D、10 |
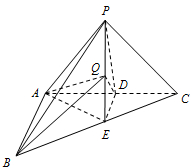 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2
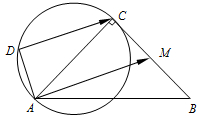 如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则
如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则