题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}-{(x-1)^2},({x<1})\\(3-a)x+4a,({x≥1})\end{array}$为增函数,则实数a的取值范围是( )| A. | -1≤a<3 | B. | a<3 | C. | a>3或a≤-1 | D. | -1<a<3 |
分析 函数f(x)是R上的增函数,具有连续性,3-a>0,且[-(x-1)2]max≤[(3-a)x+4a]min可得a的取值范围
解答 解:由题意:函数f(x)=$\left\{\begin{array}{l}-{(x-1)^2},({x<1})\\(3-a)x+4a,({x≥1})\end{array}$是R上的增函数,
∴3-a>0,且[-(x-1)2]max≤[(3-a)x+4a]min.
即$\left\{\begin{array}{l}{3-a>0}\\{0≤3-a+4a}\end{array}\right.$,
解得:-1≤a<3.
故选A.
点评 本题考查了分段函数的性质的运用.属于中档题.

练习册系列答案
相关题目
10.程序框图如图所示,其输出的结果为( )

| A. | 2100-1 | B. | 299-1 | C. | 2100 | D. | 299 |
5.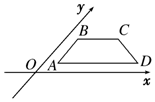 用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )
用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )
 用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )
用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )| A. | 4 cm2 | B. | 4$\sqrt{2}$ cm2 | C. | 8 cm2 | D. | 8$\sqrt{2}$ cm2 |
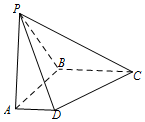 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.