题目内容
5．
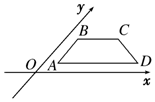用斜二测画法画出的某平面图形的直观图如图，边AB平行于y轴，BC，AD平行于x轴．已知四边形ABCD的面积为2$\sqrt{2}$ cm2，则原平面图形的面积为（ ）| A． | 4 cm2 | B． | 4$\sqrt{2}$ cm2 | C． | 8 cm2 | D． | 8$\sqrt{2}$ cm2 |
分析 根据所给的图形中∠BAD=45°，得到原图形为一个直角梯形，然后，根据高之间的关系进行求解．
解答 解：根据题意，得∠BAD=45°，原图形为一个直角梯形；
且上下底面的边长和BC、AD相等，高为梯形ABCD的高的2$\sqrt{2}$倍；
∴原平面图形的面积为$（2\sqrt{2}）^{2}$=8（cm2）．
故答案为：8cm2．
点评 本题重点考查了斜二侧画法、平面图形的面积的求解方法等知识，属于中档题．解题关键是准确理解斜二侧画法的内涵，与x轴平行的线段长度保持不变，与y轴平行的线段的长度减少为原来的一半．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
13．关于x的函数y=log${\;}_{\frac{1}{2}}$（x2-ax+2a）在[1，+∞）上为减函数，则实数a的取值范围是（ ）
| A． | （-∞，2] | B． | （-1，+∞） | C． | （-1，2] | D． | （-∞，-1） |
20．已知函数f（x）=$\left\{\begin{array}{l}-{（x-1）^2}，（{x＜1}）\\（3-a）x+4a，（{x≥1}）\end{array}$为增函数，则实数a的取值范围是（ ）
| A． | -1≤a＜3 | B． | a＜3 | C． | a＞3或a≤-1 | D． | -1＜a＜3 |
10．若函数f（x）=sin（2x+φ）满足?x∈R，f（x）≤f（$\frac{π}{6}$），则f（x）在[0，π]上的单调递增区间为（ ）
| A． | [0，$\frac{π}{6}$]与[$\frac{π}{2}$，$\frac{2π}{3}$] | B． | [$\frac{π}{3}$，$\frac{2π}{3}$] | C． | [0，$\frac{π}{6}$]与[$\frac{2π}{3}$，π] | D． | [0，$\frac{π}{6}$]与[$\frac{π}{3}$，$\frac{2π}{3}$] |