题目内容
8.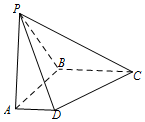 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.(1)求证:BC⊥平面PAB;
(2)求面PCD与面PAB所成锐二面角的余弦值.
分析 (Ⅰ)推导出BC⊥AB,BC⊥PA,由此能证明BC⊥平面PAB.
(Ⅱ)延长BA,CD交于Q点,过A作AH⊥PQ,垂足为H,连DH,则∠AHD是面PCD与面PBA所成的二面角的平面角,由此能求出面PCD与面PAB所成二面角的余弦值.
解答 证明:(Ⅰ)∵在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,
PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
∴BC∥AD且∠DAB=90°,BC⊥AB,
又PA⊥平面ABCD,∴BC⊥PA,
而PA∩PB=A,∴BC⊥平面PAB…(4分)
(Ⅱ)延长BA,CD交于Q点,过A作AH⊥PQ,垂足为H,连DH,
由(Ⅰ)及AD∥BC知:AD⊥平面PAQ,
∴AD⊥PQ且AH⊥PQ,
∴PQ⊥平面HAD,即PQ⊥HD.
∴∠AHD是面PCD与面PBA所成的二面角的平面角.…(6分)
由题意得$AQ=\frac{3}{2}$,$PQ=\frac{{3\sqrt{5}}}{2}$,∴$AH=\frac{AQ•PA}{PQ}=\frac{{3\sqrt{5}}}{5}$,
∴$tan∠AHD=\frac{AD}{AH}=\frac{{\sqrt{5}}}{3}$,∴cos∠AHD=$\frac{3\sqrt{14}}{14}$.
∴面PCD与面PAB所成二面角的余弦值为$\frac{{3\sqrt{14}}}{14}$.
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
19.将直线l沿y轴的负方向平移a(a>0)个单位,再沿x轴正方向平移a+1个单位得直线l',此时直线l'与l重合,则直线l'的斜率为( )
| A. | $\frac{a}{a+1}$ | B. | -$\frac{a}{a+1}$ | C. | $\frac{a+1}{a}$ | D. | -$\frac{a+1}{a}$ |
3.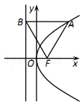 如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )
如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )
 如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )
如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )| A. | y2=$\frac{1}{2}$x | B. | y2=x | C. | y2=2x | D. | y2=4x |
13.关于x的函数y=log${\;}_{\frac{1}{2}}$(x2-ax+2a)在[1,+∞)上为减函数,则实数a的取值范围是( )
| A. | (-∞,2] | B. | (-1,+∞) | C. | (-1,2] | D. | (-∞,-1) |
20.已知函数f(x)=$\left\{\begin{array}{l}-{(x-1)^2},({x<1})\\(3-a)x+4a,({x≥1})\end{array}$为增函数,则实数a的取值范围是( )
| A. | -1≤a<3 | B. | a<3 | C. | a>3或a≤-1 | D. | -1<a<3 |