题目内容
15.函数f(x)=$\frac{{x}^{2}-2x+9}{x}$(x<0)最大值为-8.分析 f(x)=$\frac{{x}^{2}-2x+9}{x}$=$\frac{9}{x}+x-2=-[(-x)+\frac{9}{-x}]-2≤-2\sqrt{-x•\frac{9}{-x}}-2\\;\\;=-8$,再利用基本不等式即可.
解答 解:∵x<0,∴f(x)=$\frac{{x}^{2}-2x+9}{x}$=$\frac{9}{x}+x-2=-[(-x)+\frac{9}{-x}]-2≤-2\sqrt{-x•\frac{9}{-x}}-2\\;\\;=-8$=-8
故答案为:-8
点评 本题考查了应用基本不等式求最值,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.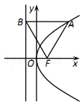 如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )
如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )
 如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )
如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )| A. | y2=$\frac{1}{2}$x | B. | y2=x | C. | y2=2x | D. | y2=4x |
20.已知函数f(x)=$\left\{\begin{array}{l}-{(x-1)^2},({x<1})\\(3-a)x+4a,({x≥1})\end{array}$为增函数,则实数a的取值范围是( )
| A. | -1≤a<3 | B. | a<3 | C. | a>3或a≤-1 | D. | -1<a<3 |
7.图中的阴影表示的集合中是( )


| A. | A∩∁UB | B. | B∩∁UA | C. | ∁U(A∩B) | D. | ∁U(A∪B) |
4.某单位为了了解用电量y(度)与气温X(0C)之间的关系,随机统计了某4天的用电量与当天气温,并作了如下的对照表:由表中数据,得回归直线方程$\hat y$=$\hat bx$+$\hat a$,若$\hat b$=-2,则$\hat a$=( )
| 气温X(0C) | 18 | 13 | 10 | -1 |
| 用电量y | 24 | 34 | 38 | 64 |
| A. | 60 | B. | 58 | C. | 62 | D. | 64 |
 如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其东北方向与它相距32海里的B处有一外国船只,且D岛位于海监船正东28$\sqrt{2}$海里处.
如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其东北方向与它相距32海里的B处有一外国船只,且D岛位于海监船正东28$\sqrt{2}$海里处.