题目内容
2.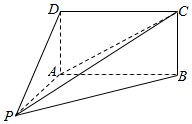 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.(Ⅰ)求证:直线DA⊥平面PAB;
(Ⅱ)求三棱锥B-PAC的体积.
分析 (I)根据矩形的性质得出AD⊥AB,AD∥BC,由BC⊥PB得出AD⊥BP,故AD⊥平面PAB;
(II)将△PAB当作棱锥的底面,则棱锥的高为BC,代入体积公式计算.
解答 (I)证明:∵四边形ABCD是矩形,∴AD⊥AB,AD∥BC.
∵∠PBC=90°,∴BC⊥PB,
∴AD⊥PB,又AB?平面APB,BP?平面ABP,AB∩BP=B,
∴DA⊥平面PAB.
(II)解:∵AD∥BC,AD⊥平面PAB,
∴BC⊥平面PAB,BC=AD=1.
∵S△PAB=$\frac{1}{2}PA•AB•sin∠PAB$=$\frac{1}{2}×1×2×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}$.
∴三棱锥B-PAC的体积V=$\frac{1}{3}{S}_{△PAB}•BC$=$\frac{1}{3}×\frac{\sqrt{3}}{2}×1$=$\frac{\sqrt{3}}{6}$.
点评 本题考查了线面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
7.等比数列{an}中,Sn表示其前n项和,a3=2S2+1,a4=2S3+1,则公比q为( )
| A. | ±2 | B. | ±3 | C. | 2 | D. | 3 |
12.现有四个函数:①y=x•sinx;②y=x•cosx;③y=x•|cosx|;④y=x•2x的图象(部分)如图,则按照从左到右的顺序,图象对应的函数序号正确的一组是( )
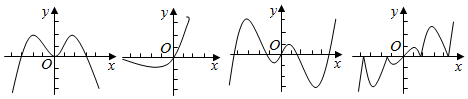
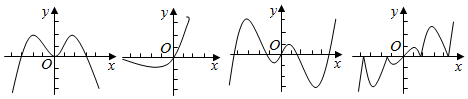
| A. | ①④③② | B. | ①④②③ | C. | ④①②③ | D. | ③④②① |
 如图,在直三棱柱ABC-A1B1C1中,D为AC的中点,∠ABC=90°,AA1=AB=2,BC=3.
如图,在直三棱柱ABC-A1B1C1中,D为AC的中点,∠ABC=90°,AA1=AB=2,BC=3.