题目内容
10.已知钝角△ABC的面积为$\frac{1}{2}$,AB=1,BC=$\sqrt{2}$,则角B=$\frac{3π}{4}$,AC=$\sqrt{5}$.分析 利用已知及三角形面积公式可求sinB,可求B=$\frac{π}{4}$或$\frac{3π}{4}$,分类讨论:当B=$\frac{π}{4}$时,由余弦定理可得AC=1,可得AB2+AC2=BC2,为直角三角形,舍去,从而利用余弦定理可得AC的值.
解答 解:∵钝角△ABC的面积为$\frac{1}{2}$,AB=1,BC=$\sqrt{2}$,
∴$\frac{1}{2}$=$\frac{1}{2}×$1×$\sqrt{2}$×sinB,解得:sinB=$\frac{\sqrt{2}}{2}$,
∴B=$\frac{π}{4}$或$\frac{3π}{4}$,
∵当B=$\frac{π}{4}$时,由余弦定理可得AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BC•cosB}$=$\sqrt{1+2-2×1×\sqrt{2}×\frac{\sqrt{2}}{2}}$=1,
此时,AB2+AC2=BC2,可得A=$\frac{π}{2}$,为直角三角形,矛盾,舍去.
∴B=$\frac{3π}{4}$,由余弦定理可得AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BC•cosB}$=$\sqrt{1+2+2×1×\sqrt{2}×\frac{\sqrt{2}}{2}}$=$\sqrt{5}$,
故答案为:$\frac{3π}{4}$;$\sqrt{5}$.
点评 本题主要考查了三角形面积公式,余弦定理,勾股定理在解三角形中的应用,考查了分类讨论思想和转化思想的应用,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
14.给出下列四个问题:
①求方程ax2+bx+c=0的解;
②判断直线和圆的位置关系;
③给三名同学的成绩排名次;
④求两点间的距离.
其中不需要用条件语句来描述其算法的有( )
①求方程ax2+bx+c=0的解;
②判断直线和圆的位置关系;
③给三名同学的成绩排名次;
④求两点间的距离.
其中不需要用条件语句来描述其算法的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.已知全集U={0,1,2,3,4},集合A={0,2,4},B={1,2,3},则A∩(∁UB)为( )
| A. | {0,4} | B. | {2,3,4} | C. | {0,2,4} | D. | {0,2,3,4} |
20.小明试图将一箱中的24瓶啤酒全部取出,每次小明在取出啤酒时只能取出三瓶或四瓶啤酒,那么小明取出啤酒的方式共有 种.( )
| A. | 18 | B. | 27 | C. | 37 | D. | 212 |
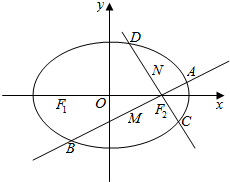 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.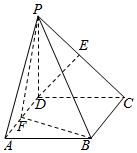 四棱锥P-ABCD中,四边形ABCD为正方形,PD⊥平面ABCD,PD=DA=2,F,E分别为AD、PC的中点.
四棱锥P-ABCD中,四边形ABCD为正方形,PD⊥平面ABCD,PD=DA=2,F,E分别为AD、PC的中点.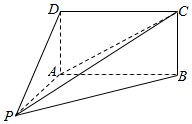 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.