题目内容
6.在等比数列{an}中,a1+a2+…+a5=27,$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{5}}$=3,则a3=3.分析 设出等比数列的公比,把已知等式化为关于a3和q的等式,作比求得a3的值.
解答 解:设等比数列{an}的公比为q,
由a1+a2+…+a5=27,$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{5}}$=3,
得$\frac{{a}_{3}}{{q}^{2}}+\frac{{a}_{3}}{q}+{a}_{3}+{a}_{3}q+{a}_{3}{q}^{2}=27$,①
$\frac{{q}^{2}}{{a}_{3}}+\frac{q}{{a}_{3}}+\frac{1}{{a}_{3}}+\frac{1}{{a}_{3}q}+\frac{1}{{a}_{3}{q}^{2}}=3$,②
两式相除,可得${{a}_{3}}^{2}=9$,
∴a3=±3.
当a3=-3时,∵a1+a2+…+a5=27>0,
∴a2>0,此时q<0,代入①不成立,
∴a3=3.
故答案为:3.
点评 本题考查等比数列的通项,考查学生的计算能力,是基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
16.已知等差数列1,a,b,又4,a+2,b+1为等比数列,求该等差数列的公差( )
| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
14.给出下列四个问题:
①求方程ax2+bx+c=0的解;
②判断直线和圆的位置关系;
③给三名同学的成绩排名次;
④求两点间的距离.
其中不需要用条件语句来描述其算法的有( )
①求方程ax2+bx+c=0的解;
②判断直线和圆的位置关系;
③给三名同学的成绩排名次;
④求两点间的距离.
其中不需要用条件语句来描述其算法的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.用M(A)表示非空数集A中元素的最大值,m(A)表示非空数集A中元素的最小值,定义ξ(A,B)为集合A,B的距离,且ξ(A,B)=min{|m(A)-M(B)|,|M(A)-m(B)|},若P={1,2},Q={x|(x2-mx)(x2+mx-2)=0}且ξ(P,Q)=1,则实数m的所有可能取值为( )
| A. | -1,0,1,2 | B. | 0,1 | C. | -1,0 | D. | -1,2 |
5.已知全集U={0,1,2,3,4},集合A={0,2,4},B={1,2,3},则A∩(∁UB)为( )
| A. | {0,4} | B. | {2,3,4} | C. | {0,2,4} | D. | {0,2,3,4} |
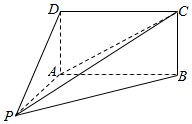 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.