题目内容
11.在△ABC中,内角A,B,C对的边长分别是a,b,c,cosB+(cosA-$\sqrt{3}$sinA)cosC=0(1)求C的值;
(2)若c=2,求a+2b的取值范围.
分析 (1)cosB+(cosA-$\sqrt{3}$sinA)cosC=0,可得-cos(A+C)+cosAcosC-$\sqrt{3}$sinAcosC=0,可化为tanC=$\sqrt{3}$,即可得出C的值;
(2)利用正弦定理把a+2b转化为含有角A的三角函数,运用辅助角公式化积后求得范围.
解答 解:(1)cosB+(cosA-$\sqrt{3}$sinA)cosC=0,
∴-cos(A+C)+cosAcosC-$\sqrt{3}$sinAcosC=0,
化为sinAsinC=$\sqrt{3}$sinAcosC,
∵sinA≠0,
∴sinC=$\sqrt{3}$cosC,
∵cosC≠0,∴tanC=$\sqrt{3}$,
∵C∈(0,π).
解得C=$\frac{π}{3}$;
(2)∵c=2,且C=$\frac{π}{3}$,
∴由$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=\frac{2}{sin\frac{π}{3}}=\frac{4\sqrt{3}}{3}$,
得$a=\frac{4\sqrt{3}}{3}sinA,b=\frac{4\sqrt{3}}{3}sinB$,
则a+2b=$\frac{4\sqrt{3}}{3}[sinA+2sin(\frac{2π}{3}-A)]$
=$\frac{4\sqrt{3}}{3}(sinA+\sqrt{3}cosA+sinA)$
=$\frac{4\sqrt{3}}{3}(2sinA+\sqrt{3}cosA)$=$\frac{4\sqrt{21}}{3}sin(A+θ)$(tan$θ=\frac{\sqrt{3}}{2}$),
∵$0<A<\frac{2π}{3}$,∴θ<A+θ$<\frac{2π}{3}+θ$,
则当A=$\frac{2π}{3}$,sinθ=$\sqrt{\frac{3}{7}}$,cos$θ=\frac{2}{\sqrt{7}}$时,
(a+2b)min=$\frac{4\sqrt{21}}{3}×\frac{\sqrt{3}}{\sqrt{7}}=4$;
当A$+θ=\frac{π}{2}$时,$(a+2b)_{max}=\frac{4\sqrt{21}}{3}$.
∴a+2b的取值范围为[4,$\frac{4\sqrt{21}}{3}$].
点评 本题考查了余弦定理、两角和差的正弦公式、诱导公式、三角函数的内角和定理,考查了推理能力与计算能力,属于中档题.

 天天向上口算本系列答案
天天向上口算本系列答案①求方程ax2+bx+c=0的解;
②判断直线和圆的位置关系;
③给三名同学的成绩排名次;
④求两点间的距离.
其中不需要用条件语句来描述其算法的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 18 | B. | 27 | C. | 37 | D. | 212 |
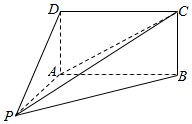 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.