题目内容
7．等比数列{an}中，Sn表示其前n项和，a3=2S2+1，a4=2S3+1，则公比q为（ ）| A． | ±2 | B． | ±3 | C． | 2 | D． | 3 |
分析 由a3=2S2+1，a4=2S3+1，两式相减可得：a4-a3=2a3，即可得出．
解答 解：由a3=2S2+1，a4=2S3+1，两式相减可得：a4-a3=2a3，可得q=$\frac{{a}_{4}}{{a}_{3}}$=3，
故选：D．
点评 本题考查了等比数列的通项公式、递推关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
名师点拨卷系列答案
相关题目
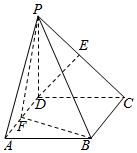四棱锥P-ABCD中，四边形ABCD为正方形，PD⊥平面ABCD，PD=DA=2，F，E分别为AD、PC的中点．
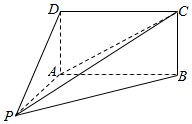如图，四棱锥P-ABCD的底面ABCD为矩形，且PA=AD=1，AB=2，∠PAB=120°，∠PBC=90°．
12．已知集合A={-1，0，1}，B={y|y=x2-x，x∈A}，则A∩B=（ ）
| A． | ?{0}? | B． | {2} | C． | ?{0，1}? | D． | {-1，0} |
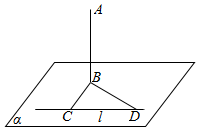如图所示，直线AB垂直平面α于点B，直线l在平面α内，点C，D在l上，∠BCD=90°，∠CDB=45°，AB=80cm，CD=60cm．求点A到直线l的距离．