题目内容
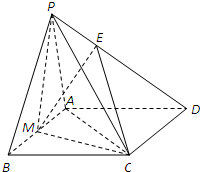 在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.
在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.(1)求证:平面PAB⊥平面PMC;
(2)求证:直线PB∥平面EMC.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)根据已知中,PA=PB.底面ABCD是菱形点M是AB的中点,根据等边三角形的‘三线合一’的性质,我们易得到AB⊥平面PMC,再由面面垂直的判定定理,即可证明结论;
(2)连BD交MC于F,连EF,由CD=2BM,CD∥BM,我们可以得到△CDF∽△MBF,根据三角形相似的性质,可以得到DF=2BF.再根据DE=2PE,结合平行线分线段成比例定理,易判断EF∥PB,结合线面平行的判定定理,即可得到结论.
(2)连BD交MC于F,连EF,由CD=2BM,CD∥BM,我们可以得到△CDF∽△MBF,根据三角形相似的性质,可以得到DF=2BF.再根据DE=2PE,结合平行线分线段成比例定理,易判断EF∥PB,结合线面平行的判定定理,即可得到结论.
解答:
证明:(1)∵PA=PB,M是AB的中点.
∴PM⊥AB.(2分)
∵底面ABCD是菱形,∴AB=AC.
∵∠ABC=60°.
∴△ABC是等边三角形.
则:CM⊥AB
又∵PM∩CM=M
∴AB⊥平面PAB
∴平面PAB⊥平面PMC
(2)连结BD交MC于F,连结EF
由CD=2BM CD∥BM
易得:△CDF∽△MBF
∴DF=2BF
DE=2PE
∴EF∥PB
EF?平面EMC PB?平面EMC
∴PB∥平面EMC
∴PM⊥AB.(2分)
∵底面ABCD是菱形,∴AB=AC.
∵∠ABC=60°.
∴△ABC是等边三角形.
则:CM⊥AB
又∵PM∩CM=M
∴AB⊥平面PAB
∴平面PAB⊥平面PMC
(2)连结BD交MC于F,连结EF
由CD=2BM CD∥BM
易得:△CDF∽△MBF
∴DF=2BF
DE=2PE
∴EF∥PB
EF?平面EMC PB?平面EMC
∴PB∥平面EMC

点评:本题考查的知识要点:线面垂直的判定定理和性质定理,面面垂直的判定定理,线面平行的判定定理,及三角形的相似问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={0,1,2},B={1,2,3},则∁(AUB)(A∩B)=( )
| A、{0,3} |
| B、{1,2} |
| C、∅ |
| D、{0,1,2,3} |
设集合S={x||x|<5},T={x|x2+4x-21<0},则S∩T=( )
| A、{x|-7<x<-5} |
| B、{x|3<x<5} |
| C、{x|-5<x<3} |
| D、{x|-7<x<5} |
已知函数f(x)=
,若关于x的方程f(x)=a(x+1)有三个不相等的实数根,则实数a的取值范围是( )
|
A、[
| ||
| B、(0,+∞) | ||
| C、C(0,1) | ||
D、(0,
|
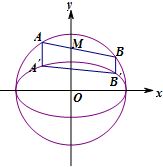 如图,设AB、A′B′分别是圆O:x2+y2=4和椭圆C:
如图,设AB、A′B′分别是圆O:x2+y2=4和椭圆C: