题目内容
设集合S={x||x|<5},T={x|x2+4x-21<0},则S∩T=( )
| A、{x|-7<x<-5} |
| B、{x|3<x<5} |
| C、{x|-5<x<3} |
| D、{x|-7<x<5} |
考点:交集及其运算
专题:函数的性质及应用
分析:本题可先对集合S、T进行化简,再求出它们的交集,得到本题结论.
解答:
解:∵集合S={x||x|<5},
∴S={x|-5<x<5},
∵集合T={x|x2+4x-21<0},
∴T={x|-7<x<3},
∴S∩T={x|-5<x<3}.
故选C.
∴S={x|-5<x<5},
∵集合T={x|x2+4x-21<0},
∴T={x|-7<x<3},
∴S∩T={x|-5<x<3}.
故选C.
点评:本题考查了集合的交集运算,本题难度不大,属于基础题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则这个几何体的体积为( )
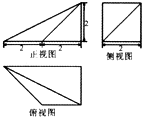

A、
| ||
B、
| ||
| C、8 | ||
| D、4 |
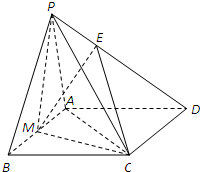 在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.
在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.