题目内容
已知实数x,y满足x2+y2=4(y≥0),则m=
x+y的取值范围是 .
| 3 |
考点:直线与圆的位置关系
专题:直线与圆
分析:首先,设圆的参数方程:
,(θ为参数,0≤θ≤π),然后,转化成三角函数的性质,结合辅助角公式进行求解其范围.
|
解答:
解:设
,(θ为参数,0≤θ≤π),则
m=
x+y=2
cosθ+2sinθ,
=4sin(θ+
),
∵0≤θ≤π,
∴
≤θ+
≤
,
∴-
≤sin(θ+
)≤1,
∴-2
≤4sin(θ+
)≤4,
∴m∈[-2
,4].
故答案为:[-2
,4].
|
m=
| 3 |
| 3 |
=4sin(θ+
| π |
| 3 |
∵0≤θ≤π,
∴
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴-
| ||
| 2 |
| π |
| 3 |
∴-2
| 3 |
| π |
| 3 |
∴m∈[-2
| 3 |
故答案为:[-2
| 3 |
点评:本题重点考查了直线与圆的位置关系、圆的参数方程等知识,属于中档题.

练习册系列答案
相关题目
已知全集∪={1,2,3,4,5,6},集合A={1,3,4,5},B={5,6},则∁U(A∪B)=( )
| A、{1,3,4} |
| B、{5,6} |
| C、{1,3,4,5,6} |
| D、{2} |
设sin(
+θ)=
,则sin2θ等于( )
| π |
| 4 |
| 1 |
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
记数列{an}的前n项和为Sn,若不等式an2+
≥ma12对任意等差数列{an}及任意正整数n都成立,则实数m的最大值为( )
| Sn2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
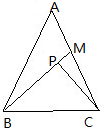 如图,在△ABC中,AB=AC=3
如图,在△ABC中,AB=AC=3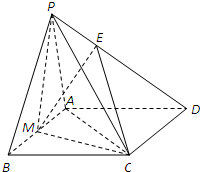 在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.
在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.