题目内容
设函数f(x)=2ax2+(a+4)x+lnx(a∈R).
(1)若a=
,求f(x)在点(1,f(1))处的切线方程;
(2)若a为整数,且函数的y=f(x)图象与x轴交于不同的两点,试求a的值.
(1)若a=
| 1 |
| 5 |
(2)若a为整数,且函数的y=f(x)图象与x轴交于不同的两点,试求a的值.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)a=
代入函数解析式,求出导函数,得到函数在x=1时的导数,求出f(1)的值,然后利用直线方程的点斜式得答案;
(2)把函数的y=f(x)图象与x轴交于不同的两点转化为其最大值大于0,然后利用导数求其最大值,解关于a的不等式得答案.
| 1 |
| 5 |
(2)把函数的y=f(x)图象与x轴交于不同的两点转化为其最大值大于0,然后利用导数求其最大值,解关于a的不等式得答案.
解答:
解:(1)a=
,则f(x)=
x2+
x+lnx,
f′(x)=
x+
+
.
f′(1)=
+
+1=6.
又f(1)=
+
=
.
∴f(x)在点(1,f(x))处的切线方程为y-
=6(x-1).
即30x-5y-7=0;
(2)由f(x)=2ax2+(a+4)x+lnx(a∈R).
得x>0,
f′(x)=4ax+a+4+
=
.
当a≥0时,f′(x)>0,
f(x)在(0,+∞)上为增函数;
当a<0时,可知x∈(0,-
)时f′(x)>0,x∈(-
,+∞)时,f′(x)<0.
∴x∈(0,-
)时,f(x)为增函数,x∈(-
,+∞)时,f(x)为减函数.
故当x=-
时函数有极大值,也是最大值.
由f(-
)=2a×(-
)2+(a+4)(-
)+ln(-
)=ln(-
)-
-1>0,
得ln(-
)>
+1.
由a为整数,
验证a=-1时,ln(-
)=0,
+1=-1,满足ln(-
)>
+1.
当a<-1时,ln(-
)<0,
+1≥0,不满足ln(-
)>
+1.
∴a的值为-1.
| 1 |
| 5 |
| 2 |
| 5 |
| 21 |
| 5 |
f′(x)=
| 4 |
| 5 |
| 21 |
| 5 |
| 1 |
| x |
f′(1)=
| 4 |
| 5 |
| 21 |
| 5 |
又f(1)=
| 2 |
| 5 |
| 21 |
| 5 |
| 23 |
| 5 |
∴f(x)在点(1,f(x))处的切线方程为y-
| 23 |
| 5 |
即30x-5y-7=0;
(2)由f(x)=2ax2+(a+4)x+lnx(a∈R).
得x>0,
f′(x)=4ax+a+4+
| 1 |
| x |
| (ax+1)(4x+1) |
| x |
当a≥0时,f′(x)>0,
f(x)在(0,+∞)上为增函数;
当a<0时,可知x∈(0,-
| 1 |
| a |
| 1 |
| a |
∴x∈(0,-
| 1 |
| a |
| 1 |
| a |
故当x=-
| 1 |
| a |
由f(-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 2 |
| a |
得ln(-
| 1 |
| a |
| 2 |
| a |
由a为整数,
验证a=-1时,ln(-
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
| 2 |
| a |
当a<-1时,ln(-
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
| 2 |
| a |
∴a的值为-1.
点评:本题考查了利用导数求过曲线上某点处的切线方程,考查了利用导数求函数的最值,体现了数学转化思想方法,是中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
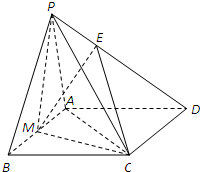 在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.
在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.