题目内容
已知函数f(x)=
,若关于x的方程f(x)=a(x+1)有三个不相等的实数根,则实数a的取值范围是( )
|
A、[
| ||
| B、(0,+∞) | ||
| C、C(0,1) | ||
D、(0,
|
考点:分段函数的应用
专题:计算题,数形结合,函数的性质及应用
分析:作出函数f(x)的图象,关于x的方程f(x)=a(x+1)有三个不相等的实数根,即为直线y=a(x+1)与曲线y=
相交时,与f(x)的图象有三个交点,求出直线与曲线y=
相切时的斜率,即可得到a的取值范围.
| x |
| x |
解答:
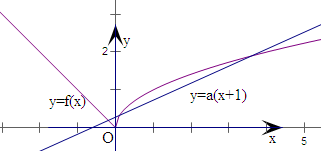 解:作出函数f(x)的图象,如右图:
解:作出函数f(x)的图象,如右图:
作出直线y=a(x+1),则直线恒过(-1,0),
关于x的方程f(x)=a(x+1)有三个不相等的实数根,即为当直线与曲线y=
相交时,
与f(x)的图象有三个交点,
当直线与曲线y=
相切时,设切点为(m,
),
则y′=
•
,则切线斜率为
•
=a,
又a(m+1)=
,由此解得,a=
(负的舍去),
故a的取值范围是(0,
).
故选D.
 解:作出函数f(x)的图象,如右图:
解:作出函数f(x)的图象,如右图:作出直线y=a(x+1),则直线恒过(-1,0),
关于x的方程f(x)=a(x+1)有三个不相等的实数根,即为当直线与曲线y=
| x |
与f(x)的图象有三个交点,
当直线与曲线y=
| x |
| m |
则y′=
| 1 |
| 2 |
| 1 | ||
|
| 1 |
| 2 |
| 1 | ||
|
又a(m+1)=
| m |
| 1 |
| 2 |
故a的取值范围是(0,
| 1 |
| 2 |
故选D.
点评:本题考查分段函数及运用,考查分段函数的图象和应用,考查数形结合的思想方法,以及运用导数求切线方程,属于中档题.

练习册系列答案
相关题目
记数列{an}的前n项和为Sn,若不等式an2+
≥ma12对任意等差数列{an}及任意正整数n都成立,则实数m的最大值为( )
| Sn2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=alnx-x+
的定义域内无极值,则实数a的取值范围( )
| a+3 |
| x |
| A、[3,-2] |
| B、[-2,6] |
| C、[-3,6] |
| D、[-3,+2] |
抛物线 x2=y的准线方程是( )
| A、4x+1=0 |
| B、4y+1=0 |
| C、2x+1=0 |
| D、2y+1=0 |
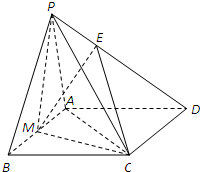 在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.
在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.