题目内容
已知在平面直角坐标系xOy中,点M到点F(2,0)的距离比它到y轴的距离多2,记点M的轨迹为C.
(1)求轨迹为C的方程;
(2)设斜率为k的直线l过定点P(-4,2),求直线l与轨迹C恰好有一个公共点,两个公共点,三个公共点时k的相应取值范围.
(1)求轨迹为C的方程;
(2)设斜率为k的直线l过定点P(-4,2),求直线l与轨迹C恰好有一个公共点,两个公共点,三个公共点时k的相应取值范围.
考点:直线与圆锥曲线的综合问题,圆锥曲线的轨迹问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设出M点的坐标,直接由题意列等式,整理后即可得到M的轨迹C的方程;
(2)设出直线l的方程为y-1=k(x+2),和(1)中的轨迹方程联立化为关于y的一元二次方程,求出判别式,再在直线y-1=k(x+2)中取y=0得到x0=-
-4.然后分判别式小于0、等于0、大于0结合x0<0求解使直线l与轨迹C恰好有一个公共点、两个公共点、三个公共点时k的相应取值范围.
(2)设出直线l的方程为y-1=k(x+2),和(1)中的轨迹方程联立化为关于y的一元二次方程,求出判别式,再在直线y-1=k(x+2)中取y=0得到x0=-
| 2 |
| k |
解答:
解:(1)设M(x,y),依题意得:|MF|=|x|+2,即
=|x|+2,
化简得,y2=4|x|+4x.
∴点M的轨迹C的方程为y2=
;
(2)在点M的轨迹C中,记C1:y2=8x(x≥0),C2:y=0(x<0).
依题意,可设直线l的方程为y-2=k(x+4).
代入抛物线方程,可得ky2-8y+16(2k+1)=0.
①当k=0时,此时y=2,把y=2代入轨迹C的方程,得x=
.
故此时直线l:y=2与轨迹C恰好有一个公共点(
,2).
②当k≠0时,方程ky2-8y+16(2k+1)=0的判别式为△=-64(2k2+k-1).
设直线l与x轴的交点为(x0,0),
则由y-2=k(x+4),取y=0得x0=-
-4.
若△<0,x0=-
-4<0,解得k<-1或k>
.
即当k<-1或k>
时,直线l与C1没有公共点,与C2有一个公共点,
故此时直线l与轨迹C恰好有一个公共点.
若△=0,x0=-
-4<0或△>0,x0=-
-4≥0,解得k=-1或k=
或-
≤k<0.
即当k=-1或k=
时,直线l与C1只有一个公共点,与C2有一个公共点.
当-
≤k<0时,直线l与C1有两个公共点,与C2无公共点.
故当k=-1或k=
或-
≤k<0时,直线l与轨迹C恰好有两个公共点.
若△>0,x0=-
-4<0,解得-1<k<-
或0<k<
.
即当-1<k<-
或0<k<
时,直线l与C1有两个公共点,与C2有一个公共点.
此时直线l与C恰有三个公共点.
| (x-2)2+y2 |
化简得,y2=4|x|+4x.
∴点M的轨迹C的方程为y2=
|
(2)在点M的轨迹C中,记C1:y2=8x(x≥0),C2:y=0(x<0).
依题意,可设直线l的方程为y-2=k(x+4).
代入抛物线方程,可得ky2-8y+16(2k+1)=0.
①当k=0时,此时y=2,把y=2代入轨迹C的方程,得x=
| 1 |
| 2 |
故此时直线l:y=2与轨迹C恰好有一个公共点(
| 1 |
| 2 |
②当k≠0时,方程ky2-8y+16(2k+1)=0的判别式为△=-64(2k2+k-1).
设直线l与x轴的交点为(x0,0),
则由y-2=k(x+4),取y=0得x0=-
| 2 |
| k |
若△<0,x0=-
| 2 |
| k |
| 1 |
| 2 |
即当k<-1或k>
| 1 |
| 2 |
故此时直线l与轨迹C恰好有一个公共点.
若△=0,x0=-
| 2 |
| k |
| 2 |
| k |
| 1 |
| 2 |
| 1 |
| 2 |
即当k=-1或k=
| 1 |
| 2 |
当-
| 1 |
| 2 |
故当k=-1或k=
| 1 |
| 2 |
| 1 |
| 2 |
若△>0,x0=-
| 2 |
| k |
| 1 |
| 2 |
| 1 |
| 2 |
即当-1<k<-
| 1 |
| 2 |
| 1 |
| 2 |
此时直线l与C恰有三个公共点.
点评:本题考查轨迹方程,考查了直线与圆锥曲线的关系,体现了分类讨论的数学思想方法,重点是做到正确分类,是中档题.

练习册系列答案
相关题目
设sin(
+θ)=
,则sin2θ等于( )
| π |
| 4 |
| 1 |
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
记数列{an}的前n项和为Sn,若不等式an2+
≥ma12对任意等差数列{an}及任意正整数n都成立,则实数m的最大值为( )
| Sn2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
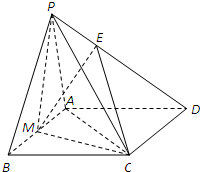 在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.
在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.