题目内容
在复平面内，复数z=（
-1）+（2x-1）i的对应点位于第二象限，则实数x的范围是（ ）
| x |
| A、（1，+∞） |
| B、（-∞，0） |
| C、（0，1） |
| D、（-∞，0）∪（1，+∞） |
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：直接由复数z的实部小于0且虚部大于0列不等式组，然后求解简单的无理不等式和指数不等式得答案．
解答：
解：∵复数z=（
-1）+（2x-1）i的对应点位于第二象限，
则
，解得0＜x＜1．
∴实数x的范围是（0，1）．
故选：C．
| x |
则
|
∴实数x的范围是（0，1）．
故选：C．
点评：本题考查了复数的代数表示法及其几何意义，考查了简单的无理不等式和指数不等式的解法，是基础的计算题．
练习册系列答案
相关题目
如图给出的是计算1+
+
+…+
的值的一个程序框图，其中判断框内应填入的条件是（ ）
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 11 |
| A、i＜12 | B、i＞11 |
| C、i＜11 | D、i≤6 |
已知集合A={-1，0，1}，B={x|x+1＞0}，那么A∩B等于（ ）
| A、{0，1} |
| B、{-1，0，1} |
| C、（-1，+∞） |
| D、[-1，+∞） |
设i为虚数单位，复数z的共轭复数为
，且（
-1）（1+i）=2i，则复数z的模为（ ）
. |
| z |
. |
| z |
| A、5 | ||
B、
| ||
| C、2-i | ||
| D、1 |
阅读如图所示的程序框图，运行相应的程序．若输入的x∈[0，2），则输出的结果可能是（ ）
| A、-1 | B、0 | C、1.5 | D、3 |
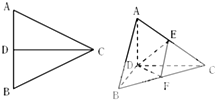已知正△ABC的边长为a，CD是AB边上的高，E、F分别是AC和BC边的中点，现将△ABC沿CD翻折成直二面角A-DC-B，如图所示．