题目内容
甲、乙两人在罚球线投球命中的概率分别为
与
,甲、乙两人在罚球线各投球一次.
(1)求这两次投球中都命中的概率;
(2)求这两次投球中至少一次命中的概率.
| 1 |
| 2 |
| 2 |
| 5 |
(1)求这两次投球中都命中的概率;
(2)求这两次投球中至少一次命中的概率.
考点:互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)记“甲投一次命中”为事件A,“乙投一次命中”为事件B,则P(A)=
,P(B)=
,P(
)=
,P(
)=
,进而根据“甲、乙两人各投球一次,都命中”的事件为A∩B,代入相互独立事件概率乘法公式,得到答案;
(2)事件“这两次投球中至少一次命中“的对立事件“甲、乙两人在罚球线各投球一次均不命中”,利用对立事件概率减法公式,可得答案.
| 1 |
| 2 |
| 2 |
| 5 |
| A |
| 1 |
| 2 |
| B |
| 3 |
| 5 |
(2)事件“这两次投球中至少一次命中“的对立事件“甲、乙两人在罚球线各投球一次均不命中”,利用对立事件概率减法公式,可得答案.
解答:
解:(1)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,
则P(A)=
,P(B)=
,P(
)=
,P(
)=
.
∵“甲、乙两人各投球一次,都命中”的事件为A∩B,且是相互独立的,
∴P(A∩B)=P(A)•P(B)=
×
=
.
答:甲、乙两人在罚球线各投球一次,都命中的概率为
.
(2)∵事件“这两次投球中至少一次命中“的对立事件“甲、乙两人在罚球线各投球一次均不命中”,
事件“甲、乙两人在罚球线各投球一次均不命中”的概率为
=
×
=
,
∴甲、乙两人在罚球线各投球一次至少有一次命中的概率P=1-
=1-
=
.
则P(A)=
| 1 |
| 2 |
| 2 |
| 5 |
| A |
| 1 |
| 2 |
| B |
| 3 |
| 5 |
∵“甲、乙两人各投球一次,都命中”的事件为A∩B,且是相互独立的,
∴P(A∩B)=P(A)•P(B)=
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 5 |
答:甲、乙两人在罚球线各投球一次,都命中的概率为
| 1 |
| 5 |
(2)∵事件“这两次投球中至少一次命中“的对立事件“甲、乙两人在罚球线各投球一次均不命中”,
事件“甲、乙两人在罚球线各投球一次均不命中”的概率为
. |
| P |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
∴甲、乙两人在罚球线各投球一次至少有一次命中的概率P=1-
. |
| P |
| 3 |
| 10 |
| 7 |
| 10 |
点评:本题考查的知识点是互斥事件的概率加法公式,对立事件的概率减法公式,分析事件之间的关系是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合A={-1,0,1},B={x|x+1>0},那么A∩B等于( )
| A、{0,1} |
| B、{-1,0,1} |
| C、(-1,+∞) |
| D、[-1,+∞) |
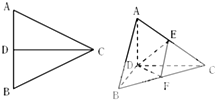 已知正△ABC的边长为a,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
已知正△ABC的边长为a,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.