题目内容
若A={x|y=log2（x-2）}，B={y|y=|x|}，则A∩B=（ ）
| A、（0，+∞） |
| B、[0，+∞） |
| C、（2，+∞） |
| D、[0，2） |
考点：交集及其运算
专题：集合
分析：求出集合A，B，利用集合的基本运算即可得到结论．
解答：
解：A={x|y=log2（x-2）}={x|x＞2}，B={y|y=|x|}={y|y≥0}，
则A∩B={x|x＞2}，
故选：C
则A∩B={x|x＞2}，
故选：C
点评：本题主要考查集合的基本运算，根据条件求出A，B是解决本题的关键，比较基础．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知集合A={-1，0，1}，B={x|x+1＞0}，那么A∩B等于（ ）
| A、{0，1} |
| B、{-1，0，1} |
| C、（-1，+∞） |
| D、[-1，+∞） |
阅读如图所示的程序框图，运行相应的程序．若输入的x∈[0，2），则输出的结果可能是（ ）
| A、-1 | B、0 | C、1.5 | D、3 |
设函数f（x）（x∈R）满足f（-x）=f（x），f（x）=f（2-x），且当x∈[0，1]时，f（x）=x3．又函数g（x）=|cos（πx）|，则函数h（x）=g（x）-f（x）在[-
，
]上的零点个数为（ ）
| 1 |
| 2 |
| 3 |
| 2 |
| A、5 | B、6 | C、7 | D、8 |
已知sinα-cosα=
，则cos2（
-α）=（ ）
| 1 |
| 3 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
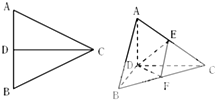已知正△ABC的边长为a，CD是AB边上的高，E、F分别是AC和BC边的中点，现将△ABC沿CD翻折成直二面角A-DC-B，如图所示．