题目内容
某种产品有3只次品和6只正品,每次取出一只测试,直到3只次品全部测出为止,求第三只次品在第6次测试时被发现的不同的测试情况有多少种.
考点:排列、组合的实际应用
专题:应用题,排列组合
分析:本题意指第6次测试的产品一定是次品,并且是最后一个次品,因而第6次测试应算是特殊位置了,可以分步完成,第一步:第6次测试的次品有几种可能; 第二步:前5次有一件正品有几种可能; 第三步:前5次有几种顺序;最后根据乘法公式计算可得共有几种可能.
解答:
解:对3只次品编序为1,2,3.
则第6次抽到其中任一件次品有
=3种情况.
前5次有2次是次品,3次是正品共有
=20种可能.
前5次测试中的顺序有
=120种可能.
∴由分步计数原理即得共有3×20×120=7200种可能.
则第6次抽到其中任一件次品有
| C | 1 3 |
前5次有2次是次品,3次是正品共有
| C | 2 2 |
| C | 3 6 |
前5次测试中的顺序有
| A | 5 5 |
∴由分步计数原理即得共有3×20×120=7200种可能.
点评:本题涉及一类重要问题,即问题中既有元素的限制,又有排列的问题,一般是先选元素(即组合)后排列

练习册系列答案
相关题目
如图给出的是计算1+
+
+…+
的值的一个程序框图,其中判断框内应填入的条件是( )

| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 11 |

| A、i<12 | B、i>11 |
| C、i<11 | D、i≤6 |
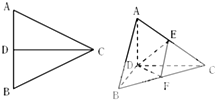 已知正△ABC的边长为a,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
已知正△ABC的边长为a,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.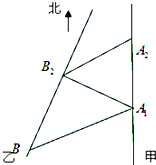 如图,甲船以每小时15
如图,甲船以每小时15