题目内容
已知四边形ABCD是菱形，若对角线
=（1，2），
=（-2，λ），则λ的值是（ ）
| AC |
| BD |
| A、-4 | B、4 | C、-1 | D、1 |
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：由于四边形ABCD是菱形，可得对角线AC⊥BD，即
⊥
．利用向量垂直与数量积的关系即可得出．
| AC |
| BD |
解答：
解：∵四边形ABCD是菱形，
∴AC⊥BD．
∵对角线
=（1，2），
=（-2，λ），
∴
•
=1×（-2）+2λ=0，
解得λ=1．
故选：D．
∴AC⊥BD．
∵对角线
| AC |
| BD |
∴
| AC |
| BD |
解得λ=1．
故选：D．
点评：本题考查了向量垂直与数量积的关系、菱形的性质，属于基础题．
练习册系列答案
相关题目
函数y=
的定义域是（ ）
| 4-log2x |
| A、（0，2] |
| B、（0，16] |
| C、（-∞，2] |
| D、（-∞，16] |
若正数x，y，z满足x2+4y2=z+3xy，则当
取最大值时，
+
-
的最大值为（ ）
| xy |
| z |
| 1 |
| x |
| 1 |
| 2y |
| 1 |
| z |
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
运行如图所示的程序框图，则输出的所有实数对（x，y）所对应的点都在函数（ ）
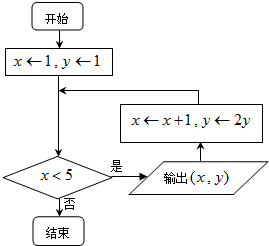
| A、y=x+1的图象上 |
| B、y=2x的图象上 |
| C、y=2x的图象上 |
| D、y=2x-1的图象上 |
i为虚数单位，若复数z=
，z的共轭复数为
，则z•
=（ ）
| 1+2i |
| 2-i |
| z |
| z |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
不等式x（x-2）≤0的解集是（ ）
| A、[0，2） |
| B、[0，2] |
| C、（-∞，0]∪[2，+∞） |
| D、（-∞，0]∪（2，+∞） |