题目内容
已知实数x,y满足:
,z=|2x-2y-1|,则z的取值范围是( )
|
A、[
| ||
| B、[0,5] | ||
| C、[0,5) | ||
D、[
|
考点:简单线性规划
专题:数形结合,不等式的解法及应用
分析:由约束条件作出可行域如图,令u=2x-2y-1,由线性规划知识求出u的最值,取绝对值求得z=|u|的取值范围.
解答:
解:由约束条件
作可行域如图,
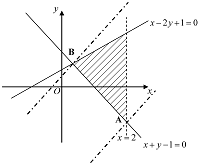
联立
,解得
,
∴A(2,-1),
联立
,解得
,
∴B(
,
).
令u=2x-2y-1,
则y=x-
-
,
由图可知,当y=x-
-
经过点A(2,-1)时,直线y=x-
-
在y轴上的截距最小,
u最大,最大值为u=2×2-2×(-1)-1=5;
当y=x-
-
经过点B(
,
)时,直线y=x-
-
在y轴上的截距最大,
u最小,最小值为u=2×
-2×
-1=-
.
∴-
≤u<5,
∴z=|u|∈[0,5).
故选:C.
|

联立
|
|
∴A(2,-1),
联立
|
|
∴B(
| 1 |
| 3 |
| 2 |
| 3 |
令u=2x-2y-1,
则y=x-
| u |
| 2 |
| 1 |
| 2 |
由图可知,当y=x-
| u |
| 2 |
| 1 |
| 2 |
| u |
| 2 |
| 1 |
| 2 |
u最大,最大值为u=2×2-2×(-1)-1=5;
当y=x-
| u |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| u |
| 2 |
| 1 |
| 2 |
u最小,最小值为u=2×
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
| 3 |
∴-
| 5 |
| 3 |
∴z=|u|∈[0,5).
故选:C.
点评:本题考查了简单的线性规划,考查了数学转化思想方法,求z得取值范围,转化为求目标函数u=2x-2y-1的取值范围,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
不等式
≥0的解集是( )
| 2-x |
| x-1 |
| A、(-∞,1)∪[2,+∞) |
| B、(-∞,1]∪[2,+∞) |
| C、[1,2] |
| D、(1,2] |
幂函数f(x)的图象过点(4,2),那么f(8)的值为( )
A、2
| ||
B、2
| ||
| C、64 | ||
D、
|
已知向量
=(1,cosα),
=(2,1)且
∥
,则锐角α的大小为( )
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|x<3},B={x|log2x<2},则A∩B=( )
| A、(-1,3) |
| B、(0,4) |
| C、(0,3) |
| D、(-1,4) |
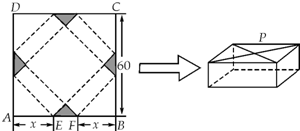 如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为
如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为