题目内容
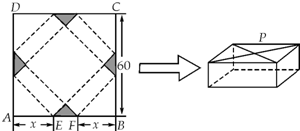 如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为
如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为考点:基本不等式在最值问题中的应用
专题:函数的性质及应用
分析:根据题意,用x分别表示出包装盒的底面边长和高,将侧面积表示为关于x的二次函数,利用二次函数性质求解即可.
解答:
解:∵AE=FB=xcm,AB=60cm,
∴EF=(60-2x)cm,
又∵阴影部分为等腰直角三角形,
∴包装盒侧面高为
(60-2x)=(30
-
x)cm,
由勾股定理得,
包装盒底边长为
xcm.
则侧面积为S侧=4(30
-
x)
x
=-8x2+240x
=-8(x-15)2+1800,
∴当x=15cm时,包装盒的侧面积最大,最大面积为1800cm2.
故答案为:15.
∴EF=(60-2x)cm,
又∵阴影部分为等腰直角三角形,
∴包装盒侧面高为
| ||
| 2 |
| 2 |
| 2 |
由勾股定理得,
包装盒底边长为
| 2 |
则侧面积为S侧=4(30
| 2 |
| 2 |
| 2 |
=-8x2+240x
=-8(x-15)2+1800,
∴当x=15cm时,包装盒的侧面积最大,最大面积为1800cm2.
故答案为:15.
点评:本题考查实际模型中数据的提取和分析能力,以及函数性质的灵活应用,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知实数x,y满足:
,z=|2x-2y-1|,则z的取值范围是( )
|
A、[
| ||
| B、[0,5] | ||
| C、[0,5) | ||
D、[
|
下列说法错误的是( )
| A、命题“若x2-5x+6=0,则x=2”的逆否命题是“若x≠2,则x2-5x+6≠0” | ||
| B、已知命题p和q,若p∨q为假命题,则命题p与q中必一真一假 | ||
C、若x,y∈R,则“x=y”是“xy≥(
| ||
| D、若命题p:?x0∈R,x02+x0+1<0,则¬p:?x∈R,x2+x+1≥0 |
现给出一个算法的算法语句如下,此算法的运行结果是( )


| A、11 | B、12 | C、13 | D、14 |