题目内容
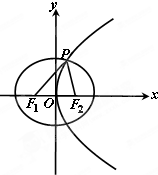 已知离心率为
已知离心率为| 1 |
| 2 |
(Ⅰ)求椭圆C1的标准方程;
(Ⅱ)若过焦点F2的直线l与抛物线C2交于A,B两点,问在椭圆C1上且在直线l外是否存在一点M,使直线MA,MF2,MB的斜率依次成等差数列,若存在,请求出点M的坐标,若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:( I)由已知得:F2(1,0),e=
=
,由此能求出椭圆C1的方程.
( II)设A(x1,y1),B(x2,y2),M(x0,y0),设直线AB的方程为:x=ny+1,由
,得y2-4ny-4=0,由此能求出椭圆上存在M(-2,0),M(2,0)M(-1,
)和M(-1,-
)都符合条件.
| c |
| a |
| 1 |
| 2 |
( II)设A(x1,y1),B(x2,y2),M(x0,y0),设直线AB的方程为:x=ny+1,由
|
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:( I)由已知得:F2(1,0),
e=
=
,
解得c=1,a=2,
∴椭圆C1的方程为:
+
=1.…(5分)
( II)设A(x1,y1),B(x2,y2),M(x0,y0),
设直线AB的方程为:x=ny+1,
kMA+kMB=
+
=2kMF2=
…(7分)
∴
=
,
∴- (y1+y2)(x0-1)2+ny0(y1+y2)(x0-1)+2ny1y2(x0-1)=2n2y0y1y2…(10分),
由
,得y2-4ny-4=0,
∴y1+y2=4n,y1y2=-4,…(11分)
∴n(x0+1)(x0-ny0-1)=0,
∵直线AB不经过F2(1,0),∴x0-ny0-1≠0,∴n=0或x0=-1…(13分)
当n=0时,椭圆上存在两点M(-2,0)或M(2,0)符合条件;
当n≠0时,则当x0=-1时,椭圆上存在两点M(-1,
)和M(-1,-
)都符合条件.…(15分)
e=
| c |
| a |
| 1 |
| 2 |
解得c=1,a=2,
∴椭圆C1的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
( II)设A(x1,y1),B(x2,y2),M(x0,y0),
设直线AB的方程为:x=ny+1,
kMA+kMB=
| y0-y1 |
| x0-x1 |
| y0-y2 |
| x0-x2 |
| 2y0 |
| x0-1 |
∴
| (y0-y1)(x0-ny2-1)+(y0-y2)(x0-ny1-1) |
| (x0-ny1-1)(x0-ny2-1) |
| 2y0 |
| x0-1 |
∴- (y1+y2)(x0-1)2+ny0(y1+y2)(x0-1)+2ny1y2(x0-1)=2n2y0y1y2…(10分),
由
|
∴y1+y2=4n,y1y2=-4,…(11分)
∴n(x0+1)(x0-ny0-1)=0,
∵直线AB不经过F2(1,0),∴x0-ny0-1≠0,∴n=0或x0=-1…(13分)
当n=0时,椭圆上存在两点M(-2,0)或M(2,0)符合条件;
当n≠0时,则当x0=-1时,椭圆上存在两点M(-1,
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查椭圆方程的求法,考查椭圆上满足条件的点的坐标的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知等差数列{an}中,a2=4,a6=12,则公差d等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
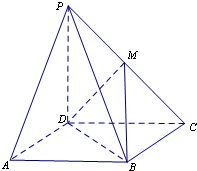 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.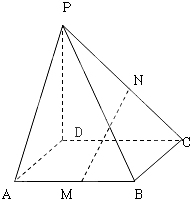 在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,M,N分别是AB,PC的中点;
在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,M,N分别是AB,PC的中点;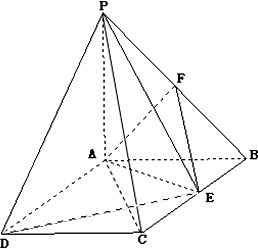 如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,点E,F分别是BC,PB的中点.
如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,点E,F分别是BC,PB的中点.