题目内容
若一系列椭圆
+
=1(n∈N*)的长轴构成数列{an},则数列{an}的前四项依次为 .
| x2 |
| (2n-17)2 |
| y2 |
| (3n-2)2 |
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:n分别用1,2,3,4,确定出椭圆的长轴,即可得出结论.
解答:
解:当n=1时,a=15,b=1,∴a1=30,
n=2时,a=13,b=4,∴a2=26,
n=3时,a=11,b=7,∴a3=22,
n=4时,a=10,b=9,a4=20.
∴数列{an}的前四项依次为30,26,22,20.
故答案为:30,26,22,20.
n=2时,a=13,b=4,∴a2=26,
n=3时,a=11,b=7,∴a3=22,
n=4时,a=10,b=9,a4=20.
∴数列{an}的前四项依次为30,26,22,20.
故答案为:30,26,22,20.
点评:本题考查椭圆的标准方程,考查数列知识的运用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
7个人站一队,其中甲在排头,乙不在排尾,则不同的排列方法有( )
| A、720 | B、600 |
| C、576 | D、324 |
已知某几何体的三视图如图,则该几何体的体积是( )


| A、80 | ||||
B、64+
| ||||
| C、104 | ||||
D、80+8
|
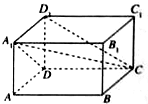 在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.
在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.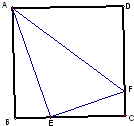 如图,△AEF是边长为x的正方形ABCD的内接三角形,已知∠AEF=90°,AE=a,EF=b,a>b,则x=
如图,△AEF是边长为x的正方形ABCD的内接三角形,已知∠AEF=90°,AE=a,EF=b,a>b,则x=