Question

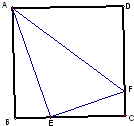如图，△AEF是边长为x的正方形ABCD的内接三角形，已知∠AEF=90°，AE=a，EF=b，a＞b，则x=

 

．

Answer 1

考点：相似三角形的性质,函数解析式的求解及常用方法,函数最值的应用

专题：函数的性质及应用,立体几何

分析：由题意，得△ABE∽△ECF，求出EC，从而求出BE，再由勾股定理求出边长AB的大小．

解答： 解：在△AEF中，∠AEF=90°，AE=a，EF=b，a＞b，正方形ABCD的边长为x；
∴△ABE∽△ECF，
∴

AB

AE

=

EC

EF

，
即

x

a

=

EC

b

，
得EC=

bx

a

，
∴BE=BC-EC=x-

bx

a

=

(a-b)x

a

，
又AB²+BE²=AE²，
即x²+

[(a-b)x]2

a2

=a²，
∴x=

a2

a2+(a-b)2

；
故答案为：

a2

a2+(a-b)2

．

点评：本题考查了利用几何图形的知识求函数解析式的问题，是基础题．